એક પ્રકાશની કિરણાવલી લાલ,લીલા અને વાદળી રંગોથી બનેલી છે.આ કિરણાવલી કોઇ કાટકોણ પ્રિઝમ પર આપાત થાય છે.લાલ,લીલા અને વાદળી રંગો માટે પ્રિઝમના દ્રવ્યનો વક્રીભવનાંક અનુક્રમે $1.39,1.44$ અને $1.47$ છે. આ પ્રિઝમ .....
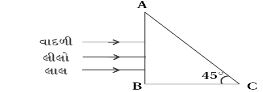

AIPMT 2015,AIEEE 2012,IIT 1989, Medium
a
As beam of light is incident normally on the face \(AB\) of the right angled prism \(ABC,\) so no refraction occurs at face \(AB\) and it passes straight and strikes the face \(AC\) at an angle of incidence, \(i=45^o\)
As beam of light is incident normally on the face \(AB\) of the right angled prism \(ABC,\) so no refraction occurs at face \(AB\) and it passes straight and strikes the face \(AC\) at an angle of incidence, \(i=45^o\)
For total reflection to take place at face \(AC\),
\(i > i_{c}\) or \(\sin i>\sin i_{c}\)
where \(i_{c}\) is the critical angle.
But as here \(i=45^o\) and \(\sin i_{c}=\frac{1}{\mu}\)
\(\therefore \quad \sin 45^o > \frac{1}{\mu}\) or \(\frac{1}{\sqrt{2}} > \frac{1}{\mu} \quad\) or \(\quad \mu>\sqrt{2}=1.414\)
As \(\mu_{\text {red }}(=1.39) < \mu(=1.414)\) while \(\mu_{\text {green }}(=1.44)\) and \(\mu_{\text {blue }}(=1.47) > \mu(=1.414),\) so only red colour will be transmitted through face \(A C\) while green and blue colours will suffer total internal reflection.
So the prism will separate red colour from the green and blue colours as shown in the following figure.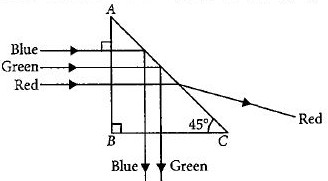
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1લેન્સથી $2.4\; m$ ના અંતરે રહેલ વસ્તુનું પ્રતિબિંબ લેન્સની પાછળ $12 \;cm$ અંતરે રહેલ પડદા પર મળે છે. $1\; cm$ જાડાઈની અને $1.5$ વક્રિભવનાંક ધરાવતી કાચની એક પ્લેટને લેન્સ અને પડદાની વચ્ચે, તેનું સમતલ પડદાને સમાંતર રહે તેમ મૂકવામાં આવે તો હવે વસ્તુ લેન્સથી કેટલે દૂર ખસેડવી પડે કે જેથી તેનું પ્રતિબિંબ પડદા પર ઝિલાય?View Solution
- 2માછલી $\sqrt 7 \,cm$ ઊંડાઇ પર છે.તો તે બહાર જોઇ શકતા ક્ષેત્રફળની ત્રિજયા કેટલા ......$cm$ હશે?View Solution
- 3$10cm$ કેન્દ્રલંબાઇ ધરાવતા બર્હિગોળ લેન્સ અને $10 cm$ કેન્દ્રલંબાઇ ધરાવતા અંર્તગોળ લેન્સને સંપર્કમાં રાખતા તંત્રની કેન્દ્રલંબાઇ કેટલી થાય?View Solution
- 4દ્વિ બહિર્ગોળ લેન્સ બે પાતળા સમતલીય બહિર્ગોળ લેન્સથી બનાવેલો છે. પહેલાં લેન્સનો વક્રીભવનાંક $1.5 $અને બીજાનો $1.2$ છે. બંન્ને વક્ર સપાટીની વક્રતાત્રિજ્યા $ R\, 14 \,cm$ છે. આ દ્વિ બહિર્ગોળ લેન્સથી $40\, cm$ દૂર પદાર્થ મૂક્લો છે. તેનું પ્રતિબિંબ કેટલા .....$cm$ મળશે?View Solution
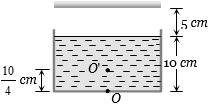
- 5આપેલ આકૃતિમાં રહેલ પાણી ભરેલા પાત્રમાં વસ્તુ $O$ નું પ્રતિબિંબ અરીસાથી કેટલા......$cm$ અંતરે મળશે?View Solution
- 6પ્રકાશની માધ્યમ $'A'$ અને $'B'$ માં ઝડપ અનુક્રમે $2.0 \times 10^{10} \,cm / s$ અને $1.5 \times 10^{10} \,cm / s$ છે. પ્રકાશકિરણ માધ્યમ $B$ માંથી $A$ માં '$\theta$ ' જેટલા આપાતકોણે દાખલ થાય છે. જો કિરણ પૂર્ણ આંતરિક પરાવર્તન અનુભવે તો ...........View Solution
- 7$10\,\,cm$ કેન્દ્રલંબાઈ ધરાવતાં અપસારી લેન્સથી એક બિંદુવત ઉદ્દગમને $15\,\,cm$ ના અંતરે મૂકેલો છે. $12\,\, cm$ કેન્દ્રલંબાઈનાં અંત:ર્ગોળ અરીસાને .......$cm$ મૂકેલ હોવો જોઈએ કે જેથી તેની જાતે વસ્તુ પર વાસ્તવિક પ્રતિબિંબ રચાયેલું હોય?View Solution
- 8View Solutionઆકૃતિમાં વિચલનકોણ અને આપાતકોણ વચ્ચેનો આલેખ દર્શાવેલ છે. આલેખ પરથી કહી શકાય કે પ્રિઝમકોણ કેટલો છે?
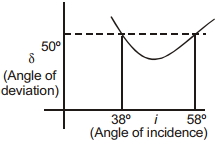
- 9$20 \mathrm{~cm}$ વક્રતા ત્રિજયા અને $1.5$ વક્રીભવનાંક ધરાવતી બહિર્ગોળ સપાટી પર એક બિંદુવત પ્રકાશ ઉદગમ માંથી પ્રકાશ આપાત થાય છે. જો આ બહિર્ગોળ સપાટીથી ઉદગમ $100 \mathrm{~cm}$ અંતર આવેલ હોય તો વસ્તુથી......... $cm$ અંતરે પ્રતિબિં રચાયView Solution
- 10View Solutionપ્રકાશ હવામાંથી કાંચમાં દાખલ થાય ત્યારે...
