લેન્સથી $2.4\; m$ ના અંતરે રહેલ વસ્તુનું પ્રતિબિંબ લેન્સની પાછળ $12 \;cm$ અંતરે રહેલ પડદા પર મળે છે. $1\; cm$ જાડાઈની અને $1.5$ વક્રિભવનાંક ધરાવતી કાચની એક પ્લેટને લેન્સ અને પડદાની વચ્ચે, તેનું સમતલ પડદાને સમાંતર રહે તેમ મૂકવામાં આવે તો હવે વસ્તુ લેન્સથી કેટલે દૂર ખસેડવી પડે કે જેથી તેનું પ્રતિબિંબ પડદા પર ઝિલાય?
AIEEE 2012, Diffcult
a
The focal length of the lens
The focal length of the lens
\(\frac{1}{f} = \frac{1}{v} - \frac{1}{u}\) \( = \frac{1}{{12}} + \frac{1}{{240}}\) \( = \frac{{20 + 1}}{{240}} = \frac{{21}}{{240}}\)
\(f=\frac{240}{21}\, \mathrm{cm}\)
Shift \( = t\left( {1 - \frac{1}{\mu }} \right)\) \( \Rightarrow 1\left( {1 - \frac{1}{{3/2}}} \right) = 1 \times \frac{1}{3}\)
Now \(v^{\prime}=12-\frac{1}{3}=\frac{35}{3} \,\mathrm{cm}\)
Now the object distance \(u\).
\(\frac{1}{u} = \frac{3}{{35}} - \frac{{21}}{{240}}\) \( = \frac{1}{5}\left[ {\frac{3}{7} - \frac{{21}}{{48}}} \right]\)
\(\frac{1}{u}=\frac{1}{5}\left[\frac{48-49}{7 \times 16}\right]\)
\(u=-7 \times 16 \times 5=-560\, \mathrm{cm}=-5.6\, \mathrm{m}\)
shift \(=5.6-2.4=3.2 \;cm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્થાનાંતર રીતમાં $f$ કેન્દ્રલંબાઈના લેન્સનો ઉપયોગ કરવામાં આવે છે અને વસ્તુ અને પડદા વચ્ચેનું અંતર $60\, cm$ છે. કેન્દ્રલંબાઈનું શક્ય મૂલ્ય ........ $cm$ છે ?View Solution
- 2$60^o$ નો પ્રિઝમકોણ ધરાવતા પ્રિઝમ પર ${15^o}$ ના ખૂણે કિરણ આપાત કરતાં ${55^o}$ નું વિચલન અનુભવે છે. તો નિર્ગમનકોણ કેટલો થશે?View Solution
- 3બર્હિગોળ લેન્સ દ્વારા વસ્તુનું પ્રતિબિંબ $4 cm$ ઊંચાઇનું મળે છે.હવે લેન્સને બીજા સ્થાને મૂકતાં વસ્તુનું પ્રતિબિંબ $16 cm$ ઊંચાઇનું મળે છે,તો વસ્તુની ઊંચાઇ કેટલા .....$cm$ હશે?View Solution
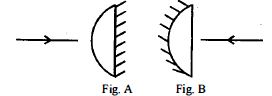
- 4આકૃતિ$-A$ માં દર્શાવ્યા મુજબ એક સમતલ બહિર્ગોળ લેન્સની સમતલ સપાટી પર ચાંદીનો ઢોળ ચડાવવામાં આવે ત્યારે તેની કેન્દ્રલંબાઈ $28\, cm$ મળે છે. જો તે જ લેન્સની આકૃતિ$-B$ માં દર્શાવ્યા મુજબ વક્ર સપાટી પર ઢોળ ચડાવવામાં આવે ત્યારે તેની કેન્દ્રલંબાઈ $10\, cm$ મળે છે. તો આ લેન્સના દ્રવ્યનો વક્રીભવનાંક કેટલો હશે?View Solution
- 5View Solutionનીચેનામાંથી ક્યુ વિધાન સાચુ છે ?
- 6View Solutionપોલા કાચના ગોળામાંથી ગોળીય અરીસો બનાવવામાં આવે છે. અરીસાની સામે વસ્તુ મુક્તા પ્ર્તિબિંબ અને મોટવણી
- 7એક માણસ $11\,\, km$ અંતરે રહેલાં બે થાંભલા સ્પષ્ટ જોઈ શકે છે. તો થાંભલા વચ્ચેનું ન્યૂનત્તમ અંતર ........$ m$ હોવું જોઈએ?View Solution
- 8પાતળા બહિર્ગોળ લેન્સ માટે વક્રતાત્રિજ્યા અનુકુમે $15 \mathrm{~cm}$ અને $30 \mathrm{~cm}$ છે. લેન્સની કેન્દ્ર લંબાઈ $20 \mathrm{~cm}$ હોય તો દ્રવ્યનો વક્રીભવનાંક. . . . . . . હશે.View Solution
- 9જ્યારે $60°$ પ્રિઝમકોણના પ્રિઝમ પર પ્રકાશનું કિરણ આપાત થાય તે ન્યૂનત્તમ વિચલન અનુભવે છે અને તેનો વક્રીભવનાંક $\sqrt 2 $ છે. તો આપાત કોણ .......$^o$ થશે.View Solution
- 10પાણી $\left(\mu=\frac{4}{3}\right)$ ના તળાવની સપાટીએ ઉભા થાંભલાની લંબાઈ $24\, cm$ છે. તો પાણીની સપાટીની નીચે રહેલી માછલીને થાંભલાની ટોચ સપાટીથી ......... $cm$ અંતરે ઉપર દેખાશે ?View Solution
