એક પ્રક્રિયા માટે જરૂરી $NO_2$ એ $CCl_4$ માં $N_2O_5$ ના નીચેના સમીકરણ મુજબના વિઘટનથી મળે છે.
$2N_2O_5 (g) \to 4NO_2 (g) + O_2 (g)$
$N_2O_5$ ની શરૂઆતની સાંદ્રતા $3.00\, mol\, L^{-1}$ છે. અને $30$ મિનિટ બાદ તે $2.75\, mol\, L^{-1}$ છે. તો $NO_2$ તા સર્જનનો દર ................ $mol\, L^{-1}\, min^{-1}$ જણાવો.
JEE MAIN 2019, Diffcult
Download our app for free and get started
a
\(2N_2O_5 (g) \to 4NO_2 (g) + O_2 (g)\)
\(2N_2O_5 (g) \to 4NO_2 (g) + O_2 (g)\)
\(t=0\) \(3.0\,M\)
\(t=30\) \(2.75\,M\)
\(\frac{{ - \,\Delta \,[{N_2}{O_5}]}}{{\Delta t}}\, = \,\frac{{0.25}}{{30}}\)
\(\frac{1}{2}\, \times \frac{{ - \,\Delta \,[{N_2}{O_5}]}}{{\Delta t}}\, = \frac{1}{4}\, \times \frac{{ - \,\Delta \,[N{O_2}]}}{{\Delta t}}\)
\(\frac{{\Delta \,[N{O_2}]}}{{\Delta t}}\, = \,\frac{{0.25}}{{30}}\, \times \,2\, = \,1.66\, \times \,{10^{ - 2}}\,M/\min \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
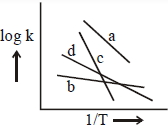
- 1ચાર જુદી જુદી પ્રક્રિયાઓ માટે વેગ અચળાંક વિરુદ્ધ $\frac{1}{\mathrm{T}}$ ના નીચેના આલેખ ધ્યાનમાં લો. તો આ પ્રક્રિયાઓની સક્રિયકરણ ઊર્જાઓ માટે નીચેના પૈકી ક્યો ક્રમ સાચો છે ?View Solution
- 2પ્રક્રિયાઓ $M, N,O$ અને $P$ માટે સક્રિયકરણ ઊર્જાનો કમ અનુક્રમે $E_M < E_N < E_O < E_P$ છે. તો કઇ પ્રક્રિયા માટે $K_{310}/K_{300}$ મહતમ થશે ?View Solution
- 3View Solutionનીચેનામાંથી કયો આલેખ સક્રિયકરણ ઊર્જાનું મૂલ્ય આપણને આપે છે?
- 4View Solutionઓરડાના તાપમાને હાઇડ્રોજન અને ઓક્સિજનનુ મિશ્રણ ખૂબ સ્થાયી છે. પરંતુ સ્પાર્ક કરવાથી તરત જ વિસ્ફોટ થાય છે. કારણ કે .........
- 5આર્ગોનની હાજરીમાં $N_2O$ નુ $N_2$ અને $O_2$ માં વિઘટન પ્રથમ કમની ગતિકીને અનુસરે છે. $K = 5.0 \times10^{11}\,e^{-2000/T}$ હોય તો પ્રકીયા સક્રિયકરણ ઊર્જા થશે?View Solution
- 6નીચે બે વિધાન આપેલા છે :View Solution
વિધાન $I$ : $A+B \rightarrow C$ પ્રક્રિયા માટે વેગ નિયમ, વેગ $(r)=k[A]^2[B]$ છે. જ્યારે $A$ અને $B$ એમ બંને ની સાંદ્રતા બમણી કરવામાં આવે છે ત્યારે પ્રક્રિયા વેગ વધી ને " $x$ " ગણો થાય છે.
વિધાન $II$ :
(Image)
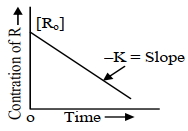
આકૃતિ " " $y$ " ક્રમ પ્રક્રિયા માટે સાંદ્રતામાં તફ઼ાવત સામે સમયનો આલેખ દર્શાંવે છે. $x+y$ નું મૂલ્ય . . . . . છે.
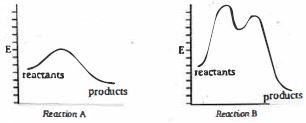
- 7View Solutionનીચેની બે પ્રક્રિયાઓ માટે, કયુ વિધાન સાચું છે?
- 8View Solutionજો સાંદ્રતા મોલ/લિટરમાં દર્શાવવામાં આવે તો પ્રથમક્રમની પ્રક્રિયા માટે વેગ અચળાંકનો એકમ........ છે.
- 9નીચે આપેલ માહિતી પરથી $H_2 + I_2\rightarrow 2HI$ પ્રક્રિયા માટે સક્રિયકરણ ઊર્જા .....View Solution
$T$ (in, $K$) $- 769$ , $1/T$ (in, $K^{-1}$ ) $- 1.3\times 10^{-3},$
$\log_{10}K - 2.9\,T$ (in, $K$) $- 667$, $1/T$ (in, $K^{-1}) - 1.5\times 10^{-3}$, $\log_{10}\,K - 1.1$
- 10પ્રથમ ક્રમની રાસાયણિક પ્રક્રિયાનો અર્ધઆયુ સમય $6.93$ મિનિટ છે. તો $99\%$ રાસાયણિક પ્રક્રિયા પૂર્ણ થવા માટે ........ મિનિટ જરૂરી છે. $(\log \,2 = 0.301)$View Solution