\(F=q(\vec{v} \times \vec{B})=\frac{q}{m}(\vec{P} \times \vec{B})\)
\(\Rightarrow F \propto \frac{ q }{ m }\)
thus \(F _{1}: F _{2}: F _{3}=\frac{ q _{1}}{ m _{1}}: \frac{ q _{2}}{ m _{2}}: \frac{ q _{3}}{ m _{3}}\)
\(=\frac{ e }{ m _{ p }}: \frac{ e }{2 m _{ p }}: \frac{2 e }{4 m _{ p }}\)
\(=\frac{1}{1}: \frac{1}{2}: \frac{2}{4}\)
\(=2: 1: 1\)
Now for speed calculation
\(P = constant \Rightarrow v \propto \frac{1}{ m }\)
thus \(v _{1}: v _{2}: v _{3}=\frac{1}{ m _{ p }}: \frac{1}{2 m _{ p }}: \frac{1}{4 m _{ p }}\)
\(=\frac{1}{1}: \frac{1}{2}: \frac{1}{4}\)
\(=4: 2: 1\)
Download our appand get started for free
Similar Questions
- 1વર્તુળાકાર ગુંચળાની અક્ષ પર કેન્દ્રથી અનુક્રમે $0.05\, m$ અને $0.2\, m$ અંતરે રહેલ બે બિંદુઓ આગળ ચુંબકીય ક્ષેત્રો $8:1$ નાં ગુણોત્તરમાં છે. ગુંચળાની ત્રિજ્યા ........... $m $ છે.View Solution
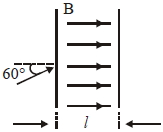
- 2$l$ લંબાઈ માં $0.3\,T$ નું ચુંબકીય ક્ષેત્ર છે. પ્રોટોન આ ક્ષેત્ર સાથે $60$ ના ખૂણે $4 \times 10^{5}\, ms ^{-1}$ ના વેગ થી દાખલ થાય છે. $10$ પરિણામમાં પ્રોટોન $l$ અંતર કાપતો હોય તો $l= ....... m$View Solution
(પ્રોટોનનું દળ $=1.67 \times 10^{-27} \,kg,$ પ્રોટોનનું વિધુતભાર $\left.=1.6 \times 10^{-19}\, C \right)$
- 3દરેક $9\, {cm}$ બાજુની લંબાઈ ધરાવતા ત્રિકોણની બાજુમાંથી $1.5\, {A}$ નો પ્રવાહ વહે છે. ત્રિકોણના કેન્દ્ર પર ચુંબકીય ક્ષેત્ર કેટલું થાય?View Solution
(પ્રવાહ સમઘડી દિશામાં વહે છે તેમ ધારો)
- 4$v$ વેગથી ગતિ કરતા $q$ વિદ્યુતભાર પર લાગતું સ્થિત વિદ્યુતકીય બળ $\left(\overrightarrow{\mathrm{F}_1}\right)$ અને ચુંબકીય બળ $\left(\overrightarrow{\mathrm{F}_2}\right)$ ને. . . . . . . .રીતે લખી શકાય.View Solution
- 5કોઈ વિસ્તારમાં ચુંબકીય ક્ષેત્ર $\overrightarrow{ B }=(\hat{i}+3 \hat{j}+4 \hat{k}) \;\mu T$ અને વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=10 \hat{ i } \;\mu V / m$ છે.તેમાં પ્રોટોન $\overrightarrow{ V }=2 \hat{ i }$ થી દાખલ થાય તો તેનો પરિણમી કુલ પ્રવેગ ($m / s ^{2}$ માં) કેટલો થશે?View Solution
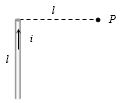
- 6આપેલ આકૃતિ માં $P $ બિંદુએ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 7ગુણાકારView Solution
$\overrightarrow{\mathrm{F}} =\mathrm{q}(\vec{v} \times \overrightarrow{\mathrm{B}})$
$=\mathrm{q} \vec{v} \times\left(\mathrm{B} \hat{i}+\mathrm{B} \hat{j}+\mathrm{B}_{0} \hat{k}\right)$
માં $\mathrm{q}=1,$ $\vec{v}=2 \hat{i}+4 \hat{j}+6 \hat{k}$ અને બળ $\overrightarrow{\mathrm{F}}=4 \hat{i}-20 \hat{j}+12 \hat{k}$
$\vec{B}$નું સંપૂર્ણ સમીકરણ શું હશે?
- 8ઇલેક્ટ્રોન ઘન $+x$ દિશામાં $6 \times 10^{6}\, ms ^{-1}$ ના વીગથી ગતિ કરે છે. વિધુતક્ષેત્ર $+ y$ દિશામાં $300 \,V / cm$ છે. ઇલેક્ટ્રોન $+ x-$ દિશામાં ગતિ કરે તે માટે ચુંબકીયક્ષેત્રનું મૂલ્ય અને દિશાView Solution
- 9$4 \pi$ મીટર લંબાઈના તારને વાળીને $6$ બાજુઓ વાળો બહુકોણ (ષટ્કોણ) બનાવવામાં આવે છે. જો બહુકોણ $4 \pi \sqrt{3} \mathrm{~A}$ વિદ્યુત્પવાહનું વહન કરતો હોય તો બહુકોણના કેન્દ્ર પરનું ચુંબકીય ક્ષેત્ર $10^{-7} x$ ટેસ્લા છે. $x$ નું મૂલ્ય____________છે.View Solution
- 10એક ગેલ્વેનોમીટરનો અવરોધ $50 \Omega$ છે અને તે મહતમ $5 \mathrm{~mA}$ પ્રવાહને પસાર થવા દે છે.તેનું $100 \mathrm{~V}$ માપી શકે તેવા વોલ્ટ મીટરમાં રુંપાંતર કરવા માટે જોડવો પડતો જરૂરી શ્રેણી અવરોધ______$\Omega$છે.View Solution
