Given, focal kngth of lens \((\mathrm{f})=15 \,\mathrm{cm}\)
object is placed at a distance \((u)=-20\, \mathrm{cm}\)
By lens formula,
\(\frac{1}{f} = \frac{1}{v} - \frac{1}{u}\)
\(\frac{1}{v} = \frac{1}{f} + \frac{1}{u}\)
\( = \frac{1}{{15}} - \frac{1}{{20}}\)
\(\frac{1}{v}=\frac{4-3}{60}\)
\({v}=60\, \mathrm{cm}\)
The image \(I\) gets formed at \(60\,\mathrm{cm}\) to the right of the lens and it wil be inverted.
The rays from the image \((I)\) formed further falls on the convex mirror forms another image This image should formed in such a way that it coincide with object at the same point due to reflection takes place by convex mirror.
Distance between lens and mirror will be \(\mathrm{d}\,=\) imagedistance \((\mathrm{v})\,-\) radius of curvature of convex mirror.
\(5=60-2 f\)
\(2 f=60-5\)
\(\mathrm{f}=\frac{55}{2}=27.5\, \mathrm{cm}\) (convex mirror)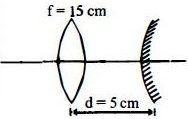
Download our appand get started for free
Similar Questions
- 1$180 cm$ લંબાઇ ધરાવતા માણસ સમતલ અરીસાથી $1m $ અંતરે છે.માણસની આંખ માથાથી $10cm$ નીચે છે,તો અરીસાની લઘુત્તમ લંબાઇ કેટલા ......$cm$ હોવી જોઈએ કે જેથી માણસ પોતાનું આખું પ્રતિબિંબ જોઇ શકે?View Solution
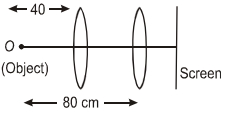
- 2સ્થાનાંતર રીતમાં સ્પષ્ટ પ્રતિબિંબ માટે લેન્સ બે સ્થાન છે. લેન્સનું પ્રથમ સ્થાન વસ્તુથી $40 \,cm$ અંતરે અને બીજુ $80 \,cm$ અંતરે છે, તો લેન્સની કેન્દ્રલંબાઈ ......... $cm$ છે.View Solution
- 3$A$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સ અને $B$ કેન્દ્રલંબાઈના અંતર્ગોળ લેન્સને એકબીજાની સંપર્કમાં મૂકેલ છે. આ તંત્રની કેન્દ્રલંબાઈ ......છે.View Solution
- 4અરીસામાં સમય $3:25$ હોય,તો સાચો સમય કેટલો હશે?View Solution
- 5સાદા ટેલિસ્કોપમાં ઓબ્જિેકિટવપીસની કેન્દ્રલંબાઇ $60cm$ અને આઇપીસની કેન્દ્રલંબાઇ $5cm$ છે. વસ્તુમાંથી આવતા કિરણો ઓબ્જિેકિટવ પાસ $2^o$ નો ખૂણો બનાવે,તો પ્રતિબિંબની કોણીય જાડાઇ કેટલા .......$^o$ થાય?View Solution
- 6$-15\;D$ અને $5\;D$ વાળા બે લેન્સ પરસ્પર સંપર્કમાં છે. આ જોડાણની કેન્દ્રલંબાઈ કેટલી થાય?View Solution
- 7$44\,cm$ લંબાઈ ધરાવતા એસ્ટ્રોનોમિકલ ટેલિસ્કોપની કોણીય મોટવણી $10$ છે. ઓબ્જિેકિટવની કેન્દ્રલંબાઇ ($cm$ માં) કેટલી હશે?View Solution
- 8પ્રકાશનું સાંકળું, અક્ષને સમાંતર અક્ષ નજીકનું કિરણ પૂંજ પડદા પર બિંદુ $I$ પાસે કેન્દ્રિત થાય છે. જાડાઈ $t$ અને વક્રીભવનાંક $\mu$ ની કાચની એક સમતલ તકતીને કિરણ પૂંજના માર્ગમાં રાખવામાં આવે છે. તો કેન્દ્રબિંદુુ કેટલા અંતરથી સ્થાનાંતરિત થાય છે ?View Solution
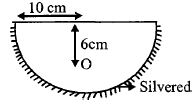
- 9$1.5$ વક્રીભવનાંક અને $10\, cm$ ત્રિજ્યા ધરાવતા અર્ધવર્તુળાકારની વક્ર સપાટી પર ચાંદીનો ઢોળ ચડાવેલ છે. તેની અક્ષ પર એક નાનો પરપોટો સમતલ સપાટીથી $6\, cm$ નીચે છે. તો અરીસા દ્વારા પરપોટાનું પ્રતિબિંબ ક્યાં મળશે?View Solution
- 10માણસ અરીસા તરફ $15\,m/s$ ના વેગથી ગતિ કરે,તો પ્રતિબિંબનો વેગ કેટલા .....$m/s$ થાય?View Solution
