એક શેલને વેગ $v_2$ સાથે સમક્ષિતિજ દિશામાં ગતિ કરતી ટ્રોલીમાંથી વેગ $v_1$ સાથે શિરોલંબ દિશામાં છોડવામાં આવે છે. જમીન પર ઉભેલી એક વ્યક્તિ શેલની ગતિને પરવલય તરીક જુએે છે, તો તેની સમક્ષિતીજ અવધી શું હશે ?
Medium
d
(d)
(d)
There is no acceleration in the horizontal direction.
\(S_x=U_x T+\frac{1}{2} a_0 \times T^2\)
\(R=U_x T \ldots (1)\)
\(S_y=U_y T+\frac{1}{2} g_y T^2\)
\(O=V_1 T-\frac{1}{2} g T^2\)
\(\Rightarrow V_1 T=\frac{1}{2} g T\)
\(T=\frac{2 V_1}{g}\)
We know,
\((R)\) range \(=(\) Horizontal velocity \(4 x) \times\) flight \(+\) time \((T)\)
i.e., \(R=4 x \times T\)
\(R=V_2 \times \frac{2 V_1}{g} \Rightarrow \frac{2 V_1 V_2}{g}\)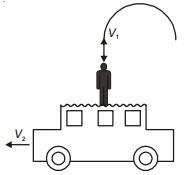
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
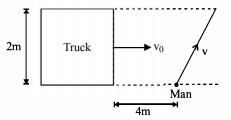
- 1$2\,m$ પહોળાઈનો ટ્રક સીધા આડા રસ્તા પર $v _0=8\,m / s$ ના નિયમિત વેગથી ગતિ કરે છે. એક રાહધરી $v$ જેટલા નિયમિત વેગ થી રોડ ક્રોસ કરે છે જ્યારે ટ્રક તેનાથી $4\,m$ દૂર હોય છે. તે સુરક્ષિત રીતે રોડ ક્રોસ કરે તે માટે $v$ ની ન્યુનત કિંમત $...........\frac{m}{s}$View Solution
- 2View Solutionઅચળ મુલ્યનું બળ બે કણની ગતિની દિશાને લંબ લાગે છે, તો પછી તેની
- 3એક ગાડી અચળ ઝડ૫ સાથે $R_1$ ત્રિજ્યા ધરાવતા વર્તુળાકાર પથ પર ફરે છે. બીજી ગાડી અચળ ઝડ૫ સાથે $R_2$ ત્રિજ્યા ધરાવતા વર્તુળાકાર પથ પર ફરે છે. જો તે બન્નેને એક રાઉન્ડ પૂર્ણ કરવાં માટે સરખો સમય લાગે તો તેની કોણીય ઝડપ અને રેખીય ઝડપનો ગુણોતર અનુક્રમે કેટલો થાય ?View Solution
- 4જ્યારે કાર સ્થિર હોય, ત્યારે ડ્રાઇવર વરસાદના ટીપાં શિરોલંબ પડતાં જોવે છે. જ્યારે તે કારને $v$ વેગથી ચલાવે ત્યારે તે વરસાદના ટીપાંને સમક્ષિતિજ સાથે $60^{\circ}$ ના ખૂણે પડતા જોવે છે. હવે કારની ઝડપ વધારીને $(1+\beta) v $ કરવામાં આવે, ત્યારે તે ખૂણો બદલાયને $45^{\circ} $ થાય છે. $\beta$ નું મૂલ્ય લગભગ કેટલું હશે?View Solution
- 5એક કણ અચળ કોણીય ઝડ૫ $12 \,rev / min$ ના દરથી $25 \,m$ ત્રિજ્યા ધરાવતા એક વર્તુળાકાર પથ પર ગતિ કરે છે. તો કણનો કોણીય પ્રવેગ ............. $rad / s ^2$ હોય.View Solution
- 6વર્તુળના પરિધ પર ગતિ કરતી વસ્તુનો કોણીય પ્રવેગ $.......$ હોય છે.View Solution
- 7એક ઉભા કાચ ધરાવતી કાર વરસાદનાં વાવાઝોડોામાં $40 \,km / hr$ ની ઝડપે ગતિ કરે છે. વરસાદ શિરોલંબ દિશામાં $20 \,m / s$ ની અચળ ઝડપે વર્ષી રહ્યો હોય તો ગાડીના કાચ પર કેટલા ખૂણે બિંદુુઓ પડતા હશે ?View Solution
- 8કારની ઝડપ $10\%$ વધારવામાં આવે છે, જો રોડનો ખૂણો અચળ રાખીને ત્રિજયા $20\,m$ માંથી ........ $m$ કરવી પડે.View Solution
- 9View Solutionનિયમિત વર્તુળમય ગતિ કરતા પદાર્થનો એક પરિભ્રમણ દરમિયાન સરેરાશ પ્રવેગ સદિશ
- 10$180\,cm$ લંબાઈની દોરીના છેડે એક પથ્થર બાંધીને તેને પ્રતિ મિનિટે સમક્ષિતિજ વર્તુળમાં $28$ ભ્રમણ કરાવવામાં આવે છે. પથ્થરના પ્રવેગનું મૂલ્ય $\frac{1936}{x}\,ms^{-2}$ છે. તો $x$ નું મૂલ્ચ $.........$ છે.View Solution
