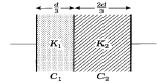
એક સમાંતર પ્લેટ કેપેસીટરની બે પ્લેટો વચ્ચે હવાનું માધ્યમ હોય ત્યારે કેપેસિટન્સ $9\;pF$ છે. બંને પ્લેટ વચ્ચેનું અંતર $d$ છે. હવે આ બંને પ્લેટ વસ્ચે બે ડાઈઈલેક્ટ્રીક દ્રવ્યો ભરવામાં આવે છે. એક ડાઈઇલેક્ટ્રીક દ્રવ્યોનો ડાઈઈલેક્ટ્રીક અચળાંક $k_{1}=3$ અને અંતર $\frac{ d }{3}$ છે. જ્યારે બીજા દ્રવ્યોનો ડાઈઈલેક્ટ્રીક અચળાંક $k _{2}=6$ અને અંતર $\frac{2 d }{3}$ છે. તો આ કેપેસિટરનું કેપેસિટન્સ ($pF$ માં) હવે કેટલું થશે ?

AIEEE 2008, Medium
d
The given capacitance is equal to two capacitances connected in series where
The given capacitance is equal to two capacitances connected in series where
\(C_{1}=\frac{k_{1} \epsilon_{0} A}{d / 3}=\frac{3 k_{1} \epsilon_{0} A}{d}=\frac{3 \times 3 \epsilon_{0} A}{d}=\frac{9 \epsilon_{0} A}{d}\)
and
\(C_{2}=\frac{k_{2} \epsilon_{0} A}{2 d / 3}=\frac{3 k_{2} \epsilon_{0} A}{2 d}=\frac{3 \times 6 \epsilon_{0} A}{2 d}=\frac{9 \epsilon_{0} A}{d}\)
The equivalent capacitance \(C_{\mathrm{eq}}\) is
\(\frac{1}{C_{\mathrm{eq}}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}=\frac{d}{9 \epsilon_{0} A}+\frac{d}{9 \epsilon_{0} A}=\frac{2 d}{9 \epsilon_{0} A}\)
\(\therefore C_{e q}=\frac{9}{2} \frac{\epsilon_{0} A}{d}=\frac{9}{2} \times 9 \,p F=40.5 \,p F\)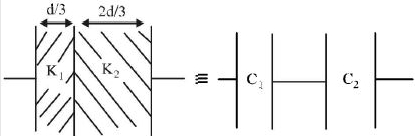
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $3\ \mu F$ કેપેસિટરને $300\, V$ ના સ્થિતિમાન સુધી વિદ્યુતભારીત કરેલ છે અને $2\ \mu F$ કેપેસિટરને $200\, V $ સુધી વિદ્યુતભારિત કરેલ છે. ત્યારે કેપેસિટરને અસમાન ધ્રુવીયતા ધરાવતી પ્લેટો સાથે સમાંતરમાં એકબીજા સાથે જોડવામાં આવે છે. જો પ્લેટો આ રીતે જોડેલી હોય, તો કેટલા ......$\mu C$ વિદ્યુતભારનો જથ્થો પસાર થતો હશે ?View Solution
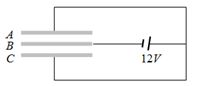
- 2ત્રણ પ્લેટો $A, B, C$ દરેક $50\, cm^2$ નું ક્ષેત્રફળ ધરાવે છે તથા તેમની વચ્ચેનું અંતર $3\ mm$ છે તો જ્યારે પ્લેટ પૂરી વિદ્યુતભારીત થાય ત્યારે તેમાં સંગ્રહાયેલ ઊર્જા....View Solution
- 3સમાંતર પ્લેટ કેપેસીટરની પ્લેટ વચ્ચેનું અંતર $d$ , પ્લેટનું ક્ષેત્રફળ $A$ અને $K$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતા દ્રવ્ય કેપેસીટરનું કેપેસીટન્સ $C_0$ છે. તેમાંથી ત્રીજા ભાગનું દ્રવ્ય $2K$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતા દ્રવ્ય વડે બદલવામાં આવે છે, કે જેથી તેમાં પરિણામી બે કેપેસીટર એક $\frac{1}{3}\,A$ ક્ષેત્રફળવાળો ,જેનો ડાઈઇલેક્ટ્રિક અચળાંક $2K$ અને બીજો $\frac{2}{3}\,A$ ક્ષેત્રફળવાળો ,જેનો ડાઈઇલેક્ટ્રિક અચળાંક $K$ થાય.જો નવા કેપેસીટરનો કેપેસીટન્સ $C$ હોય તો $\frac{C}{{{C_0}}}$ નો ગુણોત્તર કેટલો થાય?View Solution
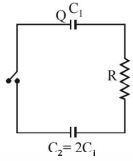
- 4આકૃતિમાં બતાવ્યા પ્રમાણે કેપેસિટરર $C _1$ અને $C _2=2 C _1$ ને તેમની વચ્ચે સ્વિય રહે તેમ પરિપથમાં જોંડલ છે. પ્રાંભમાં સ્વિચ ખુલ્લી છે અને વીજભાર $Q$ છે. $C _1$ પર સ્વીય બંધ છે. સ્થિર સ્થિતિમાં, દરેક કેપેસિટર પર વીજભાર $................$View Solution
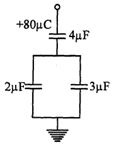
- 5આપેલ પરિપથમાં $4\ \mu F$ કેપેસિટરની ઉપરની પ્લેટને $+80\ \mu C$ કુલંબનો વિદ્યુતભાર આપવામાં આવે છે. તો સ્થિર સ્થિતિમાં $3\ \mu F$ કેપેસિટર ધરાવતા કેપેસિટરમાં ઉપરની પ્લેટનો વિદ્યુતભાર......$\mu C$View Solution
- 6એક અવાહક ધન ધાતુના ગોળાને $+Q$ વિદ્યુતભાર વડે વિદ્યુતભારીત કરેલો છે. પૃષ્ઠ પર $+Q$ વિદ્યુતભારનું વિતરણ ....... હશે.View Solution
- 7બે $6\ pF$ વાળા કેપેસીટરોને શ્રેણીમાં જોડી જોડાણને સમાંતર $5000\, V$ આપવામાં આવે છે. હવે જોડાણને તોડીને તેમને સમાંતરમાં જોડવામાં આવે તો પ્લેટો વચ્ચેનું વિદ્યુતસ્થીતીમાન....View Solution
- 8$0.6\ \mu F$ અને $0.3\ \mu F$ મૂલ્ય ધરાવતા બે કેપેસિટરોને શ્રેણીમાં $6$ વોલ્ટના ઉદગમ સાથે જોડવામાં આવે છે. તો દરેક કેપેસિટરમાં સંગ્રહિત ઊર્જાનો ગુણોત્તર શોધો.View Solution
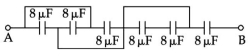
- 9આપેલ આકૃતિમાં બિંદુઓ $A$ અને $B$ વચ્ચે સમતુલ્ય સંધારકતા........... $\mu F$ છેView Solution
- 10$5\, \mu F$ કેપેસીટરને $220\,V$ વડે સંપૂર્ણ ચાર્જ કરેલ છે. પછી તેને તેમાંથી અલગ કરી તેને $2.5\;\mu F$ ના બીજા વિજભારરહિત કેપેસીટર સાથે શ્રેણીમાં જોડવામાં આવે છે. જો તેના પરના વિજભારના પુનર્વિતરણ દરમિયાન તેની ઊર્જામાં થતો ફેરફાર $\frac{ X }{100}\; J$ હોય તો $X$ નું મૂલ્ય નજીકતમ પૂર્ણાંકમાં કેટલું હશે?View Solution
