એક સ્ટીલના તારને દઢ આધાર સાથે લટકાવેલ છે.જ્યારે હવામાં તેના પર વજન લટકાવવામાં આવે ત્યારે તેની લંબાઈમાં $l_a$ જેટલો વધારો થાય અને જ્યારે તેને સંપૂર્ણ પાણીમાં ડુબાડીને વજન લટકાવવામાં આવે ત્યારે તેની લંબાઈમાં $l_w$ જેટલો વધારો થાય તો લટકાવેલ વજનની સાપેક્ષ ઘનતા કેટલી હશે?
Diffcult
b
Let \(\mathrm{V}\) be the volume of the \(1\) load and \(\rho\) its relative density
Let \(\mathrm{V}\) be the volume of the \(1\) load and \(\rho\) its relative density
So, \(Y=\frac{F L}{A \ell_{a}}=\frac{V \rho g L}{A \ell_{a}}\) \(...(1)\)
When the load is immersed in the liquid, then
\(Y=\frac{F^{\prime} L}{A \ell_{w}}=\frac{(V \rho g-V \times 1 \times g) L}{A \ell_{w}}\) \(...(2)\)
(... Now net weight \(=\) weight - upthrust) From eqs. \(( 1)\) and \((2),\) we get
\(\frac{\rho}{\ell_{\mathrm{a}}}=\frac{(\rho-1)}{\ell_{\mathrm{w}}}\) or \(\rho=\frac{\ell_{\mathrm{a}}}{\left(\ell_{\mathrm{a}}-\ell_{\mathrm{w}}\right)}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ખુલ્લી $U$ આકારની ટ્યુબમાં મરક્યુરી ભરેલી છે. જ્યારે એક બાજુ $13.6 \,cm$ જેટલું પાણી ભરવામાં આવે તો આ પરિસ્થિતિએ મરક્યુરીના લેવલમાં ................. $cm$ વધારો થશે.View Solution
- 2$10^3 \,kg / m ^3$ ધનતા અને શ્યાનતા ગુણાંક $8 \times 10^{-2} \;decapoise$ ધરાવતું પ્રવાહી $2 \,cm$ ત્રિજ્યા ધરાવતી ટ્યૂબમાંથી $2 \,m / s$ ના વેગથી વહન પામે છે તો રેનોલ્ડ અંક કેટલો ?View Solution
- 3પાણીની ટાંકીના તળિયા થી એક પત્થર ને ઉપર તરફ શિરોલંબ દિશામાં પ્રક્ષેપિત કરવામાં આવે છે. પાણીના અવરોધને અવગણતા તે ઉપર તરફ અને નીચે તરફ સરખા સમયમાં જાય છે પરંતુ જો પાણીના ખેચાણની હાજરીમાં તેને ઉપર તરફ જતાં લાગતો સમય $t_{up}$ અને નીચે તરફ જતાં લાગતો સમય $t_{down}$ હોય તો તે બંને વચ્ચેનો સંબંધ શું થાય?View Solution
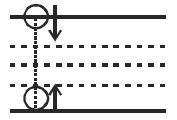
- 4બર્નુલીનું સમીકરણમાં પદોને અનુક્રમે $\frac{P}{{\rho g}} + h + \frac{1}{2}\,\frac{{{v^2}}}{g} =$ અચળView Solution
- 5પાણીનું એક નાનું બિંદુ $h$ ઊંચાઈએેથી સ્થિર અવસ્થામાંથી મુક્ત પતન કરે છે. તેનો અંતિમ વેગ એView Solution
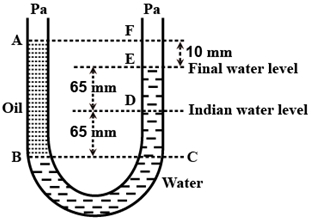
- 6એક $U$ નળી જેના બંને છેડાઓ વાતાવરણ તરફ ખુલ્લા છે, તે આંશિક રીતે પાણીથી ભરેલા છે. પાણી સાથે ન ભળી જાય તેવું તેલ નળીના એક બાજુમાં ત્યાં સુધી ભરવામાં આવે છે, જયાં સુધી બીજી બાજુમાં આવેલા પાણીની સપાટીથી $10\;mm$ ઊંચાઇ પ્રાપ્ત કરી લે છે. આ દરમિયાન પાણી પોતાનો સ્તર $65 \;mm$ જેટલું વધે છે (આકૃતિ જુઓ). તેલની ઘનતા ($kg/m^3$ માં) કેટલી હશે?View Solution
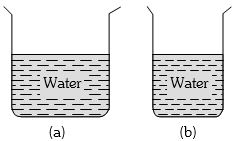
- 7View Solutionઆકૃતિ પરથી નીચેનામાંથી સાચું વિધાન કયું છે?
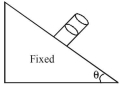
- 8એક નળાકાર પાત્રમાં ભરેલા પાણીને આકૃતિમાં બતાવ્યા મુજબ $\theta$ ખૂણાના ઢોળાવ પરની સપાટી પર છોડવામાં આવે છે. પાત્રનો સપાટી સાથેનો ઘર્ષણાંક $\mu( < \tan \theta)$ છે. તો પાણીની સપાટી દ્વારા ઢોળાવ સાથે બનેલ સંપર્કકોણ $...........$View Solution
- 9View Solutionવિધાન : વરસાદના ટીપાં ટર્મિનલ વેગ પ્રાપ્ત કરે છે.
કારણ : ગતિની દિશામાં લાગતું અચળ બળ અને વેગ પર આધાર રાખતું ગતિની વિરુદ્ધ દિશામાં લાગતું બળ હમેશા ટર્મિનલ વેગ પ્રાપ્ત કરે.
- 10એક $H$ ઊંચાઈના મોટા પાતને, $\rho$ ઘનતાના પ્રવાહીથી છલોધલ ભરવામાં આવે છે. તેની શિરોલંબ બાજુની સપાટી પર $r$ ત્રિજ્યાનું એક નાનું છિદ્ર બનાવવામાં આવે છે. (તળિયાની એકદમ નજીક) તો પ્રવાહીના દબાણને રોકવા માટે જરરી સમક્ષિતિજ બળ કેટલું હશે ?View Solution
