એક $T$ અર્ધઆયુવાળો રેડિયોએકિટવ ન્યુકિલયસ $-A $ ન્યુકિલયસ $-B$ માં ક્ષય પામે છે.$t=0 $ સમયે ન્યુકિલયસ $-A$ નથી.$t -$ સમયે $B$ ની સંખ્યા અને $A$ ની સંખ્યાનો ગુણોત્તર $0.3$ છે,તો $t$ એ _______ વડે આપવામાં આવે :
JEE MAIN 2017, Diffcult
b
Let initially there are total \(\mathrm{N}_{0}\) number of nuclei
Let initially there are total \(\mathrm{N}_{0}\) number of nuclei
At time \(\mathrm{t} \frac{N_{B}}{N_{A}}=0.3(\text { given })\)
\(\Rightarrow \quad N_{B}=0.3 N_{A}\)
\(\mathrm{N}_{0}=N_{A}+N_{B}=N_{A}+0.3 N_{A}\)
\(\therefore \quad N_{A}=\frac{\mathrm{N}_{0}}{1.3}\)
As we know \(N_{t}=N_{0} e^{-\lambda t}\)
or, \(\frac{\mathrm{N}_{0}}{1.3}=N_{0} e^{-\lambda t}\)
\(\frac{1}{1.3}=e^{-\lambda t} \Rightarrow \ln (1.3)=\lambda t\)
or, \(t=\frac{\ln (1.3)}{\lambda} \Rightarrow t=\frac{\ln (1.3)}{\frac{\ln (2)}{T}}=\frac{\ln (1.3)}{\ln (2)} T\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\beta$ - કણનો ઊર્જા વર્ણપટ્ટ [અંક $ N(E)$ જે $\beta$ - ઊર્જા $E]\, E$ વિધેય સ્વરૂપે છે. જે રેડિયો એક્ટિવ સ્ત્રોતમાંથી ઉત્સર્જાય છે?View Solution
- 2$_8O^{16}$ એ ડયુટેરોન નું શોષણ કરીને $\alpha $-કણનું ઉત્સર્જન કરે છે. અંતિમ ન્યુકિલયસ કયું થાય?View Solution
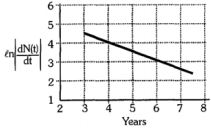
- 3રેડિયો એક્ટિવ નમૂનાનું અર્ધ આયુષ્ય એક વિધાર્થી $\ell n\,\,\left| {\frac{{dN\,\,(t)}}{{dt}}} \right|$ વિરુદ્ધ $t$ નો આલેખ છે. જો આ રેડિયો એક્ટિવ ન્યુક્લિસમાં $4.16$ વર્ષ બાદ $P$ ના ગુણાંકમાં ઘટાડો થાય છે. તો $p =$…..View Solution
- 4જો $Ge$ ના ન્યુકિલયસની ત્રિજયા ${}_4^9Be$ ના ન્યુકિલયસની ત્રિજયા કરતા બમણી છે. $Ge$ માં કેટલા ન્યુકિલઓન હશે?View Solution
- 5$ _4B{e^9} $ પરમાણુ પર $ \alpha - $ કણ આપાત કરતાં ન્યુકિલયસ $ _6{C^{12}} $ અને ____ બને.View Solution
- 6એક રેડિયો એક્ટીવ ન્યુક્લિયસનો શરૂઆતનો પરમાણુ દળાંક $A$ અને પરમાણુક્રમાંક $Z$ છે. તે $3 \alpha$ કણો અને $2$ પોઝિટ્રોન્સ ઉત્સર્જિત કરે છે. આ ઉત્સર્જન બાદ ન્યુક્લિયસમાં ન્યુટ્રોન અને પ્રોટોનની સંખ્યાનો ગુણોત્તર કેટલો થાય?View Solution
- 7રેડિયો એક્ટિવ તત્વનું અર્ધ આયુષ્ય $30$ દિવસ છે, તો $90$ દિવસમાં કેટલા ...........$\%$ ભાગનું વિખંડન થયું હશે?View Solution
- 8જો રેડિયોએકિટવ તત્ત્વનો અર્ધઆયુ સમય $T$ છે, તો $ \frac{T}{2} $ સમયે અવિભંજીત ભાગ કેટલો હશે?View Solution
- 9View Solutionઆપેલ ન્યુક્લિયસની જોડમાંથી કઈ જોડની ઇલેક્ટ્રોન રચના સમાન છે?
- 10એક રેડિયો એકિટવ ન્યુક્લિયસ બે જુદી જુદી પ્રક્રિયા દ્વારા ક્ષય પામે છે. પ્રથમ પ્રક્રિયા માટેની અર્ધઆયુ $3.0$ કલાક, જ્યારે બીજી પ્રક્રિયા માટે તે $4.5$ કલાક છે. ન્યુક્લિયસનો અસરકારક અર્ધ આયુ ........... કલાક હશે.View Solution
