એક વિદ્યુત દ્વિધ્રુવ પૂર્ણ $\vec P$ છે,જે $x$-અક્ષ સાથે $\theta $ કોણ બનાવે છે.જયારે તેને વિદ્યુતક્ષેત્ર $\overrightarrow {{E_1}} $ $=E$$\hat i$ માં મૂકતા, તે બળ- ઘૂર્ણ $\overrightarrow {{T_1}} $ =$\;\tau \hat k$ અનુભવે છે.જયારે અન્ય વિદ્યુતક્ષેત્ર $\overrightarrow {{E_2}} $ = $\sqrt 3 {E_1}\hat j$ માં મૂકતાં, તે બળ-ઘૂર્ણ $\overrightarrow {{T_2}} $ = $ - \overrightarrow {{T_1}} $ અનુભવે છે.કોણ $\theta \;$નું મૂલ્ય......$^o$ હશે.
JEE MAIN 2017, Diffcult
c
\(\mathrm{T}=\mathrm{PE} \sin \theta\) Torque experienced by the dipole in an electric field,
\(\mathrm{T}=\mathrm{PE} \sin \theta\) Torque experienced by the dipole in an electric field,
\(\quad \vec{T}=\vec{P} \times \vec{E}\)
\(\vec{p}=p \cos \theta \hat{i}+p \sin \theta \hat{j}\)
\(\vec{E}_{1}=\overrightarrow{E i}\)
\(\vec{T}_{1}=\vec{p} \times \vec{E}_{1}=(p \cos \theta \hat{i}+p \sin \theta \hat{j}) \times E(\hat{i})\)
\(\tau \hat{k}=p E \sin \theta(-\hat{k}).........(i)\)
\(\vec{E}_{2}=\sqrt{3} E_{1} \hat{j}\)
\(\left.\vec{T}_{2}=p \cos \theta \hat{i}+p \sin \theta \hat{j}\right) \times \sqrt{3} E_{1} \hat{j}\)
\(\tau \hat{k}=\sqrt{3} p E_{1} \cos \theta \hat{k}.........(ii)\)
From eqns. ( \(i\) ) and \((ii )\)
\(p E \sin \theta=\sqrt{3} p E \cos \theta\)
\(\tan \theta=\sqrt{3} \quad \therefore \quad \theta=60^{\circ}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$R$ ત્રિજ્યા વાળી એક સમાન રીતે વિદ્યુતભારિત થયેલી રિંગની અક્ષ પર લાગતું વિદ્યુતક્ષેત્રનું મહત્તમ મૂલ્ય તેના કેન્દ્રથી $h$ અંતર આગળ છે. $h$ નું મૂલ્ય હશે.View Solution
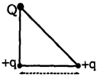
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે બે બાજુઓ સમાન હોય તેવા કાટકોણ ત્રિકોણના શિરોબિંદુઓ આગળ ત્રણ વિદ્યુતભાર $Q, +q$ અને $+q$ મૂકેલા છે. તંત્રની રચનાનું ચોખ્ખું સ્થિત વિદ્યુત શાસ્ત્રનું બળ શૂન્ય છે. જો $Q$ ........ ને સમાન છે.View Solution
- 3$8$ $\mu g$ દળ અને $39.2 \times {10^{ - 10}}$ વિદ્યુતભાર ધરાવતા ગોળાથી બનાવેલ સાદા લોલક પર સમક્ષિતિજ દિશામાં $20 \times {10^3}\ volt/meter$ વિદ્યુતક્ષેત્ર લગાવતાં,દોરી શિરોલંબ સાથે કેટલા .......$^o$ નો ખૂણો બનાવે?View Solution
- 4$10^{-4} \mathrm{~m}^2$ આડછેદનું ક્ષેત્રફળ ધરાવતા પાતળા ધાતુના તારનો $30 \mathrm{~cm}$ ત્રિજયાની વલય બનાવવામાં ઉપયોગ થાય છે. $2 \pi \mathrm{C}$ મૂલ્યનો ધન વીજભાર સમાન રીતે વલય પર વિતરીત થયેલ છે જ્યારે $30 \mathrm{pC}$ મૂલ્યનો ધન વીજભાર વલયના કેન્દ્ર પર રાખેલ છે. વલયમાં ઉદભવતું તણાવબળ_____$\mathrm{N}$ છે કે જેને લીધે વલયમાં વિકૃતિ ઉદ્ભવતી નથી. (ગુરૂત્વીય અસર અવગણો)$\left(\right.$ ને, $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \mathrm{SI}$ એકમ $)$View Solution
- 5કલ્પના કરો કે એક પ્રોટોન અને ઇલેક્ટ્રોનનો વિદ્યુતભાર થોડોક અલગ છે. જેમાંથી એક $-e$ અને બીજો $( e +\Delta e )$ છે. $d$ અંતરે (જ્યાં $d$ પરમાણુની સાઇઝ કરતાં ઘણું મોટું છે) રહેલા બે હાઇડ્રોજન પરમાણુ વચ્ચે સ્થિતવિદ્યુત બળ અને ગુરુત્વાકર્ષણ બાળાનું પરિણમી બળ શૂન્ય થવા માટે $\Delta e$ કેટલું હોવું જોઈએ? [આપેલ : હાઇડ્રોજનનું દળ $m_h= 1.67 \times 10^{-27}\, kg $]View Solution
- 6$0.1 \,\mu m$ ત્રિજ્યાનો એક વિદ્યુતભારતીત પાણીનું ટીપુ વિદ્યુતક્ષેત્રની સંતુલન અવસ્થા હેઠળ આવેલ છે. ટીપા પરનો વિદ્યુતભાર ઈલેકટ્રોનીક્સ વિદ્યુતભારને સમતુલ્ય છે. વિદ્યુતક્ષેત્રની તીવ્રતા ........$N/C$ છે.?View Solution
- 7$10\, cm$ ત્રિજ્યાનો એક ગોલીય વાહક સમાન રીતે વિતરિત $3.2 \times 10^{-7} \,C$ વિજભાર ધરાવે છે આ ગોળાના કેન્દ્રથી $15 \,cm$ અંતરે રહેલા બિંદુ પર વિદ્યુતક્ષેત્રનું માન શું હશે ?View Solution
$\left(\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} Nm ^{2} / C ^{2}\right)$
- 8સમાન વિદ્યુતભાર ધરાવતા બે સમાન ગોળાઓને એક આધારબિંદુથી સરખી લંબાઈની દોરી વડે લટકાવેલ છે. ત્યારે બે દોરી વચ્ચેનો કોણ $30^o$ છે. જ્યારે $0.8\, g\, cm^{-3}$ ઘનતાના પ્રવાહીમાં ડૂબાડવામાં આવે ત્યારે બે દોરી વચ્ચેનો કોણ ગોળાઓ હવામાં હતા તયારે જેટલો હતો તેટલો જ રહે છે. જો ગોળાઓના દ્રવ્યની ઘનતા $1.6 \,g \,cm^{-3}$ હોય તો પ્રવાહીનો ડાઈઈલેક્ટ્રિક અચળાંક ........ છે.View Solution
- 9$5\, nC$ વિદ્યુતભાર ધરાવતાં કણોને $X$- અક્ષ પર અનુક્રમે $x = 1$ $cm$, $x = 2$ $cm$, $x = 4$ $cm$ $x = 8$ $cm$ ………. મૂકેલાં છે.ઘન અને ૠણ વિદ્યુતભારને એકાંતરે મૂકેલા છે.તો ઉગમ બિંદુ પર વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
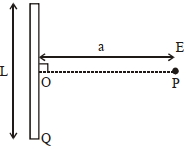
- 10આકૃતિમાં દર્શાવ્યા મુજબ $Q$ વિજભાર ધરાવતાં $L$ લંબાઈ અને એક સમાન વીજભારિત પાતળા તારનાં લંબ દ્વિભાજક પર આવેલ બિંદુ $P$ પરનું વિદ્યૂતક્ષેત્ર શોધો. બિંદુ $P$ નું સળિયાનાં કેન્દ્ર થી અંતર $a=\frac{\sqrt{3}}{2} L$ છે.View Solution