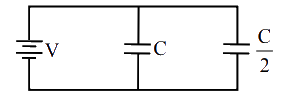
એક વિદ્યુતભારિત ગોળાની અંદરનું સ્થિત વિદ્યુતસ્થિતિમાનનું સૂત્ર $\phi=$ $ar ^{2}+ b$ છે. જ્યાં $r =$ ગોળાના કેન્દ્રથી અંતર; $a,b$ અચળાંકો છે. ગોળાની અંદર વિદ્યુતભાર ઘનતા કેટલી હોય ?
AIEEE 2011, Diffcult
d
Electric field
Electric field
\(E=-\frac{d \phi}{d r}=-2 a r.........(i)\)
By Gauss's theorem
\(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r^{2}}.........(ii)\)
From \((i)\) and \((ii)\),
\(\mathrm{q}=-8 \pi \varepsilon_{0} a r^{3}\)
\(\Rightarrow \quad d q=-24 \pi \varepsilon_{0} a r^{2} d r\)
Charge density, \(\rho=\frac{d q}{4 \pi r^{2} d r}=-6 \varepsilon_{0} a\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$C$ કેપેસિટન્સ ધરાવતાં કેપેસિટરની બે પ્લેટ વચ્ચેનું અંતર બમણું કરીને ડાઇઇલેકિટ્રક ભરતાં,નવો કેપેસિટન્સ $2C$ થાય,તો ડાઇઇલેકિટ્રક નો ડાઇઇલેકિટ્રક અચળાંક કેટલો હશે?View Solution
- 2સમાન કેપેસિટન્સ $C$ ધરાવતાં કેપેસિટરને $V_1$ અને $V_2$ વોલ્ટેજથી ચાર્જ કરીને સમાંતરમાં જોડતાં તે કેટલી ઊર્જા ગુમાવશે?View Solution
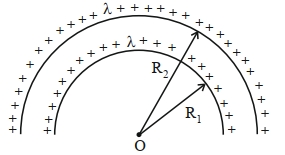
- 3સમાન રેખીય વીજભાર ધનતા $\lambda$ ધરાવતી $R _1$ અને $R _2$ ત્રિજયાની સમકેન્દ્રિય અર્ધલયોના કેન્દ્ર સ્થાને વિદ્યુત સ્થિતિમાન $.............$ છે.View Solution
- 4બે $6\ pF$ વાળા કેપેસીટરોને શ્રેણીમાં જોડી જોડાણને સમાંતર $5000\, V$ આપવામાં આવે છે. હવે જોડાણને તોડીને તેમને સમાંતરમાં જોડવામાં આવે તો પ્લેટો વચ્ચેનું વિદ્યુતસ્થીતીમાન....View Solution
- 5નીચેના વિધાન $-1$ અને વિધાન $-2$ વાંચીને યોગ્ય વિકલ્પ પસંદ કરો.View Solution
વિધાન $-1$ : એક વિદ્યુતભારિત કણ $P$ થી $Q$ તરફ ગતિ કરે છે. આ દરમિયાન વિદ્યુતક્ષેત્ર દ્વારા કણ પર થતું કાર્ય એ $P$ થી $Q$ તરફના ગતિમાર્ગ પર આધારિત નથી.
વિધાન $-2$ : બંધ માર્ગમાં ગતિ કરતાં કણ પર સંરક્ષી બળ વડે થતું કાર્ય શૂન્ય હોય છે.
- 6એક સમાંતર પ્લેટ કેપેસિટર પાસે $20\, kV$ સ્થિતિમાન અને $2 \times 10^{-4}\ \mu F$ કેપેસિટન્સ છે. જો પ્લેટનું ક્ષેત્રફળ $0.01\, m^2$ હોય અને પ્લેટો વચ્ચેનું અંતર $2\ mm$ હોય તો સ્થિતિમાન પ્રચલન શોધો.View Solution
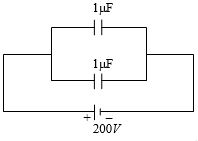
- 7આપેલ તંત્રની કુલ ઊર્જા કેટલા........$joules$ થાય?View Solution
- 8જો આ ક્ષેત્રનું સ્થિતિમાન $x, y$ યામને આધારે $V=10\,axy$ થી દર્શાવતું હોય તો વિદ્યુતક્ષેત્રની તિવ્રતાનો સદિશ કયો ગણાશે?View Solution
- 9$8\ cm$ બાજુવાળા ચોરસના શિરોબિંદુ પર વિદ્યુતભાર $\frac{{10}}{3} \times {10^{ - 9}}$ $C$ મૂકતાં કેન્દ્ર પર વોલ્ટેજ કેટલો થાય?View Solution
- 10આકૃતિમાં દર્શાવ્યા મુજબ કેપેસિટર $C$ અને $\frac{C}{2}$ ને બેટરી સાથે જોડેલા છે.આ બંને કેપેસિટરને સંપૂર્ણ ચાર્જ કરવા માટે કેટલું કાર્ય કરવું પડે?View Solution