એક વિદ્યુતભારીત વસ્તુ સાથે સંકળાયેલું વિદ્યુત ફલક્સ $\phi$ છે. આ પદાર્થને હવે ધાતુના પાત્રની અંદર મૂકવામાં આવ્યો છે. પાત્રની બહાર ફલક્સ $\phi$ કેટલું હશે?
Easy
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
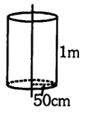
- 1$1\, mm$ ત્રિજ્યાના લાંબા સુરેખ તાર પર વિદ્યુતભાર સમાન રીતે વિતરિત થયેલો છે. તારની પ્રતિ $cm$ લંબાઈ $Q$ દીઠ વિદ્યુતભાર $Q$ કુલંબ છે. $50\, cm$ ત્રિજ્યા અને $1\, m$ લંબાઈના તારથી સંમિત રીતે ઘેરાયેલો છે. નળાકાર ના પૃષ્ઠમાંથી પસાર થતું કુલ ફલક્સ .......... છે.View Solution
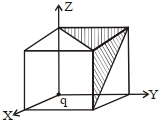
- 2આકૃતિમાં દર્શાવ્યા મુજબ $'q'$ વિજભાર ને સમઘનનાં એક ખૂણા પર ગોઠવવામાં આવ્યો છે. આચ્છાદિત ક્ષેત્રફળમાંથી પસાર થતાં સ્થિત વીજ ક્ષેત્ર $\overrightarrow{ E }$ નું ફ્લક્સ ...... હશે.View Solution
- 3$d$ વિજભારિત ગોળા વચ્ચે લાગતું બળ $F$ છે. તેને ડાઈઇલેક્ટ્રિક અચળાંક $2$ ધરાવતા પ્રવાહીમાં તેટલા અંતરે મૂકવાથી નવું બળ કેટલું થાય?View Solution
- 4ડાઈપોલ માટે પ્રત્યેક વિદ્યુતભારની કિંમત $10^{-10} \,st\, C$ અને તેમના વચ્ચેનું અંતર $1\,\mathop A\limits^o $ હોય તો તેની ડાઈપોલની ચાકમાત્રા ........ છે.View Solution
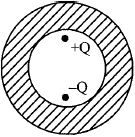
- 5આકૃતિમાં દર્શાવ્યા પ્રમાણે બે બિંદુવત વિજભાર $+Q$ અને $-Q$ ને એક ગોળીય કવચની બખોલમાં મૂકેલા છે. વિજભારને બખોલની સપાટીની નજીક અને કેન્દ્રથી વિરુદ્ધ દિશામાં મૂકેલા છે. જો $\sigma _1$ એ અંદરની સપાટી પૃષ્ઠ વિજભારઘનતા અને $Q_1$ તેના પર રહેલો કુલ વિજભાર અને $\sigma _2$ એ બહારની સપાટીની પૃષ્ઠ વિજભારઘનતા અને $Q_2$ તેના પર રહેલો કુલ વિજભાર હોય તો ...View Solution
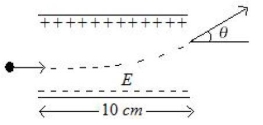
- 6બે સમાંતર પ્વેટ (તક્તિ)ની વચ્યે $10\,N/C$ નું નિયમિત વિદ્યુતક્ષેત્ર ઉત્પન્ન થાય છે. એક ઇલેક્ટોન $0.5\,eV$ ગતિઊર્જા સાથે તક્તિઓની વચ્યેના વિસ્તારમાં સંમિતિ પૂર્વક દાખલ થાય છે. દરેક તક્તિઓની લંબાઈ $10\,cm$ છે. જ્યારે ઈલેકટ્રોન આ ક્ષેત્રના વિસ્તારમાંથી બહાર નીકળે ત્યારે તેના ગતિપથના વિચલન કોણ $(\theta)$ $...........^{\circ}$ (ડિગ્રી) થશે.View Solution
- 7$R$ ત્રિજ્યા ધરાવતી રીંગ પર ધન વિદ્યુતભાર $Q$ વિતરિત થયેલ છે. $m$ દળ અને $-q$ વિદ્યુતભાર ધરાવતાં બિંદુવત કણને રીંગનાં અક્ષ પર કેન્દ્રથી $x$ અંતરે મુકેલ છે. જો તેને ત્યથી મુક્ત કરવામાં આવે અને $x < R$ હોય તો તેની સરળ આવર્તગતિનો આવર્તકાળ કેટલો થાય?View Solution
- 8$L$ મીટર બાજુવાળો ચોરસ પેપરના સમતલમાં છે. સમાન વિદ્યુતક્ષેત્ર $\vec E\;(V/m) $ પેપરના સમતલમાં છે, પણ તે ચોરસના નીચેના અડધા વિસ્તારમાં સીમિત છે. (આકૃતિ જુઓ) પૃષ્ઠ સાથે સંકળાયેલ વિદ્યુતફલક્સ $SI$ એકમમાં કેટલું હશે?View Solution
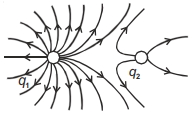
- 9View Solutionઆકૃતીમાં વિદ્યુતભાર રચનાને કારણે વિદ્યુતક્ષેત્ર રેખાઓ દર્શાવેલ છે. આ પરથી આપણો કહીં શકીએે કે
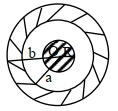
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે અંદરની ત્રિજયા $a$ અને બહારની ત્રિજયા $b$ ધરાવતા ગોળીય કવચની અંદર $R$ ત્રિજયા અને $q$ વિદ્યુતભાર ધરાવતો ધાતુનો ગોળો છે. તો વિદ્યુતક્ષેત્ર $\overrightarrow{{E}}$ વિરુદ્ધ તેના કેન્દ્ર $O$ થી અંતર $r$ સાથેનો ગ્રાફ લગભગ કેવો મળશે?View Solution
