એક વિસ્તારમાં વિદ્યુતક્ષેત્ર એકરૂપ છે. અને $\vec{E}=a \hat{i}+b \hat{j}+c \hat{k}$ વડે આપવામાં આવેલ છે. $\vec{A}=\pi R^2 \hat{i}$ ક્ષેત્રફળની સપાટી સાથે સંકળાયેલ વિદ્યુત ફલક્સ કેટલું છે?
Easy
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આકૃતીમાં દર્શાવ્યા મુજબ ત્રણ અનંત લંબાઇથી પ્લેટોને મુકેલ છે તો $P$ બિંદુ આગળ વિદ્યુત ક્ષેત્ર....View Solution
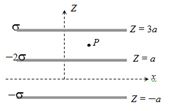
- 2View Solutionવાહક પદાર્થનો વિદ્યુતભાર બદલાતો નથી. જ્યારે.....
- 3એક સમઘન કદ $x=0, x= a , y=0, y= a$ અને $z=0, z= a$ સપાટીઓ દ્વારા ઘેરાયેલ છે. આ વિસ્તારમાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }={E_{ox}} \hat{i},$ જ્યાં $E _0=4 \times 10^4\,NC ^{-1}\,m ^{-1}$, વડે આપવામાં આવે છે. જો $a=2\,cm$ હોય તો સમઘન કદમાં સંકળાયેલ વિદ્યુતભાર $Q \times 10^{-14}\,C$ છે. $Q$ નું મૂલ્ય $........$ થશે.( $\varepsilon_0= 9 \times 10^{-12}\,C ^2 / Nm ^2$ લો.)View Solution
- 4મિલકનના ઓઇલ ડ્રોપ પ્રયોગમાં એક વિજભાર ટર્મિનલ વેગ $V$ થી ગતિ કરે છે. જો $E$ જેટલું વિદ્યુતક્ષેત્ર શિરોલંબ દિશામાં ઉપર તરફ લગાવવામાં આવે તો તે ઉપર તરફ $2V$ જેટલા ટર્મિનલ વેગથી ગતિ કરે છે. જો વિદ્યુતક્ષેત્રનું મૂલ્ય ઘટાડીને $\frac{E}{2}$ કરવામાં આવે તો આ ટર્મિનલ વેગ કેટલો થાય?View Solution
- 5મિલકનના ઓઇલ ડ્રોપ પ્રયોગમાં એક વિજભાર ટર્મિનલ વેગ $V$ થી ગતિ કરે છે. જો $E$ જેટલું વિદ્યુતક્ષેત્ર શિરોલંબ દિશામાં ઉપર તરફ લગાવવામાં આવે તો તે ઉપર તરફ $2V$ જેટલા ટર્મિનલ વેગથી ગતિ કરે છે. જો વિદ્યુતક્ષેત્રનું મૂલ્ય ઘટાડીને $\frac{E}{2}$ કરવામાં આવે તો આ ટર્મિનલ વેગ કેટલો થાય?View Solution
- 6ત્રણ બિંદુવત વીજભારો $q,-2 q$ અને $2 q , x$-અક્ષ પર $x=0, x=\frac{3}{4} R$ અને $x=R$ અંતરે અનુક્રમે ઉદગમથી મૂકેલા આકૃતિમાં દર્શાવેલ છે. જો $q =2 \times 10^{-6}\,C$ અને $R=2\,cm$ હોય તો $-2 q$ વિદ્યુતભારને અનુભવતું પરિણામી બળ ..........$N$ છે.View Solution
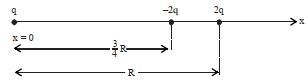
- 7$1.6 \,g$ દળના સિક્કામાંથી કેટલા ઈલેક્ટ્રોન દૂર કરવા જોઈએ કે જેથી ઉપરની દિશામાં $10^9 \,N / C$ ની તીવ્રતાના વિદ્યુતક્ષેત્ર તે તારે ?View Solution
- 8સમબાજુ ત્રિકોણ $ABC$ ના દરેક શિરોબિંદુ પર $ + \,q$ વિજભાર મૂકેલા છે તો $O$ બિંદુ પાસે વિદ્યુતક્ષેત્રની તીવ્રતા કેટલી થાય?View Solution
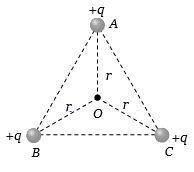
- 9જો $a$ બાજુવાળા સમઘનના કોઇ એક ખૂણા પર બિંદુવત વિદ્યુતભાર $Q$ છે, તો આ સમઘનમાંથી પસાર થતું કુલ ફલક્સ કેટલું હશે?View Solution
- 10ડાઈપોલ માટે પ્રત્યેક વિદ્યુતભારની કિંમત $10^{-10} \,st\, C$ અને તેમના વચ્ચેનું અંતર $1\,\mathop A\limits^o $ હોય તો તેની ડાઈપોલની ચાકમાત્રા ........ છે.View Solution