એક વર્તુળાકાર રિંગ $30^o$ ખૂણાવાળા ઢાળ પરથી સરક્યાં વગર ગબડે છે. તો તેનો તે ઢાળ પર રેખીય પ્રવેગ કેટલો હશે?
Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
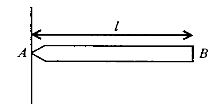
- 1એક નિયમિત સળિયો $AB$ ની લંબાઇ $l$ અને દળ $m$ છે, તે બિંદુ $A$ ને અનુલક્ષીને ભ્રમણ કરે છે. સ્થિર સળિયાને સમક્ષિતિજ સ્થિતિમાંથી મુકત કરવામાં આવે છે. બિંદુ $A$ ને અનુલક્ષીને સળિયાની જડત્વની ચાકમાત્રા $ml^2/3 $ હોય, તો સળિયાનો પ્રારંભિક કોણીય પ્રવેગ કેટલો થશે?View Solution
- 2$D$ વ્યાસ અને $L$ લંબાઈના નળાકારની લંબાઈને લંબ અને તેના ગુરૂત્વકેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
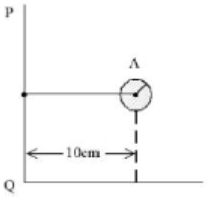
- 3ધન ગોળા $A$ અક્ષ $PQ$ ને અનુલક્ષીને ચાકગતિ કરે છે. જો ગોળાની ત્રિજ્યા $5\,cm$ હોય, તો તેની અક્ષ $PQ$ ને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા $\sqrt{x}\; cm$ થશે. અહી $x$ નું મૂલ્ય $........$ હશે.View Solution
- 4$1.5 \,m$ ત્રિજ્યા ધરાવતી એક પુલીને (ગરગડી)ને $F=\left(12 t -3 t ^{2}\right) \,N$ જેટલા સ્પર્શીય બળ (જ્યાં $t$ એ સેકન્ડમાં મપાય છે) વડે તેની અક્ષને ફરતે ભ્રમણ કરાવવામાં આવે છે. જો પુલીને તેની ભ્રમણ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $4.5 \,kg m ^{2}$ છે,તો તેની ભ્રમણની દિશા ઉલટાય તે પહેલાં પુલી દ્વારા થતા ભમણોની સંખ્યા $\frac{K}{\pi}$ છે. $K$ નું મૂલ્ય ........... હશે.View Solution
- 5View Solutionએવી પરિસ્થિતિ લો કે જેમાં એક રિંગ, નક્કર નળાકાર અને નક્કર ગોળો સમતલ ઢાળ પરથી સરક્યા વિના ગબડે છે. ધારો કે તેઓ સ્થિર સ્થિમાંથી શરૂઆત કરે છે અને તેમના વ્યાસ સમાન છે.
આ પરિસ્થિતિ માટે યોગ્ય વિધાન કયું છે
- 6$'m'$ દળના એક પદાર્થને જમીન સાથે $45^{\circ}$ ના ખૂણે $'u'$ વેગથી ફેંકવામાં આવે છે. પ્રક્ષિપ્ત બિંદુને અનુલક્ષીને મહત્તમ ઊંચાઈ પર પદાર્થનું કોણીય વેગમાન $\frac{\sqrt{2} \mathrm{mu}^2}{\mathrm{Xg}}$ વડે આપેલ છે તો $'X'$ નું મૂલ્ય ........View Solution
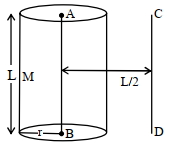
- 7$80\, {cm}$ લંબાઈ અને ${M}$ દળ ધરાવતા ઘન નળાકારની ત્રિજ્યા $20\, {cm}$ છે. આકૃતિમાં દર્શાવેલ $AB$ ને સમાંતર $CD$ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $2.7\, {kg} {m}^{2}$ હોય તો પદાર્થની ઘનતાની (${kg} / {m}^{3}$ માં) ગણતરી કરો.View Solution
- 8$m$ દળનો એક પત્થર કોઈ દોરીના છેડે બાંધીને એક સમક્ષિતિજ ઘર્ષણરહિત ટેબલ પર વર્તુળાકારે ફેરવવામાં આવે છે. પત્થરનું કોણીય વેગમાન વર્તુળના કેન્દ્રને અનુલક્ષીને અચળ રહે તેમ દોરીની લંબાઈ ધીમે ધીમે ઘટાડવામાં આવે છે. દોરીનું તણાવ $T\, = Ar^n$ (જ્યાં $A$ એ અચળાંક છે) દ્વારા આપેલ છે, એ વર્તુળની તત્કાલિન ત્રિજ્યા છે. તો $n$ ની કિંમત શું હશે?View Solution
- 9$m$ દળ અને $R$ ત્રિજ્યાનો એક પોલો ગોળો એ $\theta$ ખૂણાવાળાં ઢોળાવયુક્ત ખરબચડા સમતલ પર ગબડે છે. જો પોલો ગોળો અને ઢોળાવ વચ્ચેનો ઘર્ષણાંક નીચે તરફ ગબડે $\mu$ હોય તો,View Solution
- 10અક તંત્રમાં $m_1=3 \mathrm{~kg}$ અને $m_2=2 \mathrm{~kg}$ દળ ધરાવતા બે કણોને એકબીજાથી અમુક અંતરે રાખવામાં આવ્યા છે. $m_1$ દળ ધરાવતા કણને તંત્રના દ્રવ્યમાન કેન્દ્ર તરફ $2 \mathrm{~cm}$ જેટલો ખસેડવામાં આવે છે. તંત્રના દ્રવ્યમાન કેન્દ્રને તેના મૂળ સ્થાન ઉપર જ રાખવા માટે $m_2$ દળ ધરાવતા કણને દ્રવ્યમાન કેન્દ્ર તરફ. . . . . $cm$ અંતરથી ખસેડવો પડશે.View Solution