અક તંત્રમાં $m_1=3 \mathrm{~kg}$ અને $m_2=2 \mathrm{~kg}$ દળ ધરાવતા બે કણોને એકબીજાથી અમુક અંતરે રાખવામાં આવ્યા છે. $m_1$ દળ ધરાવતા કણને તંત્રના દ્રવ્યમાન કેન્દ્ર તરફ $2 \mathrm{~cm}$ જેટલો ખસેડવામાં આવે છે. તંત્રના દ્રવ્યમાન કેન્દ્રને તેના મૂળ સ્થાન ઉપર જ રાખવા માટે $m_2$ દળ ધરાવતા કણને દ્રવ્યમાન કેન્દ્ર તરફ. . . . . $cm$ અંતરથી ખસેડવો પડશે.
JEE MAIN 2024, Diffcult
Download our app for free and get started
d
\(\Delta \mathrm{X}_{\text {C.O.M }}=\frac{\mathrm{m}_1 \Delta \mathrm{x}_1+\mathrm{m}_2 \Delta \mathrm{x}_2}{\mathrm{~m}_1+\mathrm{m}_2}\)
\(\Delta \mathrm{X}_{\text {C.O.M }}=\frac{\mathrm{m}_1 \Delta \mathrm{x}_1+\mathrm{m}_2 \Delta \mathrm{x}_2}{\mathrm{~m}_1+\mathrm{m}_2}\)
\(\Rightarrow 0=\frac{3 \times 2+2(-\mathrm{x})}{3+2}\)
\(\Rightarrow \mathrm{x}=3 \mathrm{~cm}\)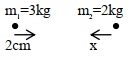
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક વર્તુળાકાર તકતી $L$ લંબાઈના ઢાળ પરથી ઉપરથી નીચે આવે છે, જ્યારે તે ઢાળ પર સરકીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{1}$ છે. જ્યારે તે ગબડીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{2}$ છે. તો $\frac{t_{2}}{t_{1}}$ નું મૂલ્ય $\sqrt{\frac{3}{x}}$ છે, તો $x$ નું મૂલ્ય કેટલું હશે?View Solution
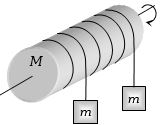
- 2$M$ દળ અને $r$ ત્રિજયા ધરાવતા નળાકાર પર $m$ દળ લટકાવતા તેનો પ્રવેગView Solution
- 3$L $ લંબાઈનો પાતળા સળિયાને એક છેડેથી લટકાવેલો છે અને તે $ n $ ભ્રમણ પ્રતિ સેકન્ડથી ચાકગતિ કરે છે. સળિયાની ચાક ગતિ ઊર્જા કેટલી થશે ?View Solution
- 4View Solutionસમાન ઊંચાઈ અને અલગ અલગ ખૂણો ધરાવતા ઢાળ પરથી ઘન ગોળાને ગબડાવતા બંને કિસ્સામાં ....
- 5$1\,kg$ દળ ધરાવતો એક નિયમિત ગોળો સમતલ સપાટી ઉપર સરક્યા સિવાય ગબડે છે. તેને $7 \times 10^{-3}\,J$ જેટલી ગતિઉર્જા છે. ગોળાના દ્રવ્યમાન કેન્દ્રની ઝડપ $...........\,cm s ^{-1}$ હશે.View Solution
- 6$'m'$ દળ અને $R $ ત્રિજ્યાનો નળાકાર તેની અક્ષ પર '$\omega$' કોણીય વેગથી ઘર્ષણ વિના ચાકગતિ કરે છે. $ v$ વેગથી ગતિ કરતો $m$ દળનો કણ તેની સાથે અથડાઇને તેની રીમ પર ચોટી જાય છે. આઘાત બાદ નળાકારનો કોણીય વેગ ગણો.View Solution
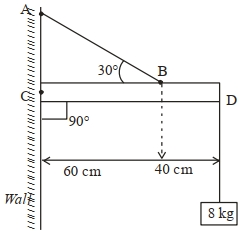
- 7એક $8\,kg$ દળ ધરાવતા પદાર્થને $2\,kg$ દળ અને $1\,m$ લંબાઈ ધરાવતા એક નિયમિત સળિયા $CD$ ના એક છેડાથી લટકાવેલ છે, સળિયાનો બીજો છેડો આકૃતિમાં દર્શાવ્યા અનુસાર ઉર્ધ્વ (શિાોલંબ) દિવાલ સાથે ટકાવેલ છ. તે સળિયાને $A B$ તાર (કેબલ) વડે અવી રીતે ટેકવેલો છે કે જથી તંત્ર સંતુલનમાં રહે. કેબલમાં તણાવ $............\,N$ હશે.(ગુરુત્વીયપ્રવેગ $g=10\,m / s ^2$ )View Solution
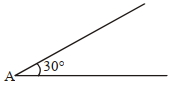
- 8$2\,kg$ દળ અને $0.5\, m$ ત્રિજ્યા ધરાવતો ગોળો $1 \,ms ^{-1}$ ના વેગથી $30^{\circ}$ ખૂણાવાળા ઢાળ પર ઉપર તરફ ગતિ કરે છે. તો તેને બિંદુ $A$ પર પાછા આવતા કેટલો સમય ($sec$) લાગશે?View Solution
- 9View Solutionઅલગ દળ, ત્રિજ્યા અને ધનતા ધરાવતા બે નક્કર ગોળાઓ એક ખરબચડા ઢોળાવ ઉપર થી સમાન સ્થિતિ હેઠળ નીચે ગબડે છે. તેમનો નીચે આવવા નો સમય તેમના થી સ્વતંત્ર છે.
- 10એક વર્તૂળાકાર તકતી $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. જો તકતી પર બાળક બેસે, તો શેનું સંરક્ષણ થશે ?View Solution