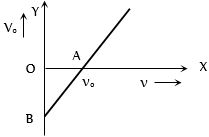
ફોટોઇલેકટ્રોનનો સ્ટોપિંગ વોલ્ટેજ ${V_0}$ વિરુધ્ધ આપાત આવૃત્તિ $ f$ નો આલેખ આપેલ છે,તો ધાતુનું વર્કફંકશન કોના જેટલો હોય?
Easy
Download our app for free and get started
a
(a) Using Einstein’s equation, \({V_0} = \left( {\frac{h}{e}} \right)\,\nu - \frac{{{W_0}}}{e}\)
(a) Using Einstein’s equation, \({V_0} = \left( {\frac{h}{e}} \right)\,\nu - \frac{{{W_0}}}{e}\)
Comparing this equation with \(y = mx + c\) We get intercept on \(-V_0\) axis \( = \frac{{{W_0}}}{e}\)
==> \(OB = \frac{{{W_0}}}{e}\)
==> \({W_0} = OB \times e\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વર્તુળાકાર કક્ષામાં ભ્રમણ કરતાં કણની કક્ષાની પરિમિતિ તે કણની દ’બ્રોગલી તરંગલંબાઈના મૂલ્ય જેટલી છે. એક વિજભારિત ચુંબકીયક્ષેત્રને લંબ ગતિ કરતાં કણની $n$ મી કક્ષાની ત્રિજ્યા કોના સમપ્રમાણમાં હશે?View Solution
- 2હાયદ્રોગેન પરમાણુમાં $3 \rightarrow 2$ સંક્રાતિ દરમિયાન ઉત્સાર્જીત વિકિરણ સોનાની સપાટી પર આપત કરીને ફોટોઇલેક્ટ્રોન ઉત્પન્ન કરવામાં આવે છે. આ ઇલેક્ટ્રોનને $5 \times 10^{-4} \,{T}$ જેટલા ચુંબકીયક્ષેત્રમાંથી પસાર કરવામાં આવે છે. ધારો કે આ ઇલેક્ટ્રોન દ્વારા ઉત્પન્ન થતાં વરુલકાર પથની મહત્તમ ત્રિજ્યા $7\, {mm}$ છે, તો ધાતુનું કાર્ય વિધેય ($eV$ માં) કેટલું હશે?View Solution
(ઇલેક્ટ્રોનનું દળ $=9.1 \times 10^{-31} \,{kg}$ )
- 3$4.8\ cm$ ત્રિજયા ધરાવતા ધાતુના ગોળા પર $200\ nm$ નો પ્રકાશ આપાત કરવામાં આવે છે.$10^3$ ફોટોન દીઠ $1$ ઇલેકટ્રોનનું ઉત્સર્જન થાય છે,તો $1 \times$ $10^{-7} \ J $ ઊર્જા આપાત કરતાં ગોળાનો વોલ્ટેજ કેટલા .............. $V$ થાય?View Solution
- 4View Solutionનીચેના પૈકીનું ક્યું વિધાન ખોટું છે?
- 5$27^oC$ અને $127^oC$ તાપમાને હાઇડ્રોજન અને હિલીયમની દ-બ્રોગ્લી તરંગલંબાઇનો ગુણોત્તર કેટલો થાય?View Solution
- 6$\alpha $ -કણ પર $0.25\; Wb/m^2$ તીવ્રતાના ચુંબકીય ક્ષેત્રની હાજરીમાં તે $0.83 \;cm$ ત્રિજયાના વર્તુળમાં ભ્રમણ કરે છે. આ કણ સાથે સંકળાયેલ દ’બ્રોગ્લી તરંગલંબાઇ ............. $\mathring A$ હશે.View Solution
- 7મહત્તમ $4.0\ eV$ ગતિઊર્જાવાળુ ફોટો ઇલેકટ્રોન ઉત્સર્જિત કરતી સપાટી પર $5.5\ eV$ ઊર્જાવાળો ફોટોન પડે છે. તો આ ઇલેકટ્રોન માટે સ્ટોપીંગ પોટેન્શીયલ............ $V$View Solution
- 8$5000\,\mathop A\limits^o $ ની તરંગલંબાઈ ધરાવતા ફોટોન ની ઊર્જા $2.5\, eV$. છે. $1\,\mathop A\limits^o $ તરંગલંબાઈ ધરાવતા $x-ray$ ના ફોટોનની ઊર્જા.View Solution
- 9હાડકાના ફ્રેકચરના અભ્યાસ માટે જોઈતા સખત ક્ષ-કિરણોની મહતમ તરંગલંબાઈ $10^{-11}\ m$ છે. તો ક્ષ-કિરણ મશીનમાં પ્રવેગીત વોલ્ટેજ .....View Solution
- 10હિલિયમ-નિયોન લેસર વડે $667 \;nm $ તરંગલંબાઇવાળો એકરંગી પ્રકાશ ઉત્પન્ન કરવામાં આવે છે. ઉત્સર્જિત પાવર $9\;mW$ છે. કોઈ ટાર્ગેટ પર આ પ્રકાશને આપાત કરવામાં આવે ત્યારે પ્રતિ સેકન્ડે આપત થતાં ફોટોનની સરેરાશ સંખ્યા કેટલી હશે?View Solution