ગોળીય અવકાશગંગાની દળ ઘનતા તેના કેન્દ્રથી લાંબા અંતર $'r'$ પર $\frac{ K }{ r }$ મુજબ બદલાય છે. એક ક્ષેત્રમાં એક નાનો તારો $R$ ત્રિજયાની વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે તો તેના માટે આવર્તકાળ $T$ અને $R$ વચ્ચેનો સંબંધ શું થાય?
JEE MAIN 2020, Diffcult
c
\(dm =\rho dv\)
\(dm =\rho dv\)
\(dm =\left(\frac{ k }{ r }\right)\left(4 \pi r ^{2} dr \right)\)
\(dm =4 \pi krdr\)
\(M =\int_{0}^{ R } d m =\int_{0}^{ R } 4 \pi krdr\)
\(M=\left.4 \pi k \frac{r^{2}}{2}\right|_{0} ^{R}\)
\(M =2 \pi k \left( R ^{2}-0\right)\)
\(M =2 \pi kR ^{2}\)
for circular motion gravitational force will provide required centripital force or
\(\frac{ GMm }{ R ^{2}}=\frac{ mv ^{2}}{ R }\)
\(\frac{G\left(2 \pi kR ^{2}\right) m }{ R ^{2}}=\frac{ mv ^{2}}{ R } \Rightarrow v =\sqrt{2 \pi GkR }\)
Time period \(\quad T =\frac{2 \pi R }{ v }\)
\(T =\frac{2 \pi R }{\sqrt{2 \pi GkR }} \propto \sqrt{ R }\)
or \(T^{2} \propto R\)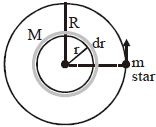
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વીની સપાટી આગળના વજન કરતાં એક તૃત્યાંશ $\left(\frac{1}{3}\right)$ વજન થાય, તે પૃથ્વીની સપાટી થી ઉંચાઈ ....... $km$ હશેView Solution
[પૃથ્વી ની ત્રિજયા $R =6400\, km , \sqrt{3}=1.732$ ]
- 2View Solutionનીચેનામાથી ક્યો ગુરુત્વસ્થિતિમાન અને પૃથ્વીના કેન્દ્રથી અંતર વચ્ચેનો ગ્રાફ છે
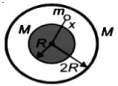
- 3$M$ દળ અને $R$ ત્રિજ્યાનો નિયમિત ગોળો એ એજ દળના પરંતુ $2 R$ ત્રિજ્યાના સમકેન્દ્રીય ગોળાકાર કવચથી આવરિત થયેલો છે. જો બિંદુવત દળ $m$ ને ગોળા દ્વારા આવરીત થયેલા ક્ષેત્રની અંદર આકૃતિમાં દર્શાવ્યા મૂજબ $x(>R)$ અંતરે મૂકેલો છે. તો કણ પરનું પરિણમી ગુરુત્વાકર્ષણ બળ કેટલું છે ?View Solution
- 4એક $S$ ઉપગ્રહ પૃથ્વીની ફરતે દીર્ઘવૃતિય કક્ષામાં ફરે છે. જો ઉપગ્રહનું દળ પૃથ્વીના દળની સાપેક્ષમાં ઘણું નાનું હોય, તો .......View Solution
- 5View Solutionકમ્યુનિકેશન ઉપગ્રહનો આવર્તકાળ ......... કલાક હોય .
- 6View Solutionજો બે બિંદુુવત્ દળોની અનંત અંતરે ગુરુત્વ સ્થિતિ ઊર્જા શૂન્ય લેવામાં આવે તો ગેલેકક્ષીની ગુરુત્વ સ્થિતિઊર્જા ..... હશે?
- 7View Solutionએક મિસાઇલને તેની નિષ્ક્રમણ ઝડપ કરતાં ઓછી ઝડપે પ્ર્ક્ષિપ્ત કરવામાં આવે તો તેની ગતિઉર્જા અને સ્થિતિઉર્જા નો સરવાળો
- 8$2 \times 10^4\,kg$ વજન ધરાવતું એક અંતરીક્ષયાન પૃથ્વીની સપાટીની નજીકની વર્તુળાકાર કક્ષામાં છોડવામાં આવે છે. ગુરુત્વાકર્ષીય ખેંચાણને દૂર કરવા માટે અવકાશયાનને કક્ષામાં આપવામાં આવતી વધારાનો વેગ ...... હશે. $\left(\right.$ જો $g =10\,m / s ^2$ અને પૃથ્વી ની ત્રિજ્યા $\left.=6400\,km \right)$View Solution
- 9એક ગ્રહ સૂર્યની આજુબાજુ લંબવૃતીય કળામાં ભ્રમણ કરે છે.જયારે તે સૂર્યથી સૌથી નજીક હોય ત્યારે તેનું સૂર્યથી અંતર $1.6 \times {10^{12}}\,m$ અને વેગ $60 \,m/s$ છે.જયારે તે સૂર્યથી સૌથી દૂર હોય ત્યારે તેનું સૂર્યથી અંતર $8 \times {10^{12}}\,m$ અને તેનો વેગ $m/s$ માં કેટલો થાય?View Solution
- 10View Solutionકેપ્લરનો બીજો નિયમ કયા નિયમના સંરક્ષણથી મળે છે.
