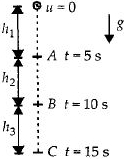
ગુરુત્વાકર્ષણમાં એક પથ્થર મુકત પતન કરે છે. તે $h_1,h_2 $ અને $ h_3$ અંતર ક્રમશ: પ્રથમ $5$ સેકન્ડમાં, પછીની $ 5 $ સેકન્ડમાં અને પછીની $5$ સેકન્ડમાં કાપે છે. $h_1,h_2 $ અને $h_3$ વચ્ચેનો સંબંધ શું થાય?
AIPMT 2013, Medium
b
\(\begin{array}{l}
\,\,\,\,\,\,\,{\rm{Distance covered}}\,by\,the\,in\,first\,5\,{\rm{second}}\,\\
\,\,\left( {i.e.t = 5\,s} \right)\,is\\
\,{h_1} = \frac{1}{2} = g{\left( 5 \right)^2} = \frac{{25}}{2}g\,\,\,\,\,\,\,...\left( i \right)\\
\,\,{\rm{Distance}}\,travelled\,by\,the\\
stone\,in\,next\,5\,\,{\rm{second}}\,\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {i.e.t = 10\,s} \right)\,is\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_1} + {h_2} = \frac{1}{2}g{\left( {10} \right)^2} = \frac{{100}}{2}g\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)\\
{\rm{Distance}}\,travelled\,by\,the\,stone\,in\,5\,{\rm{second}}\\
\left( {i.e.t = 15\,s} \right)\,\,is\\
\,\,\,\,\,\,\,\,\,\,\,\,{h_1} + {h_2} + {h_3} = \frac{1}{2}g{\left( {15} \right)^2} = \frac{{225}}{2}g\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {iii} \right)\\
Subtract\,\left( i \right)\,from\,\left( {ii} \right),\,we\,get\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{h_1} + {h_2}} \right) - {h_2} = \frac{{100}}{2}g - \frac{{25}}{2}g = \frac{{75}}{2}g\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_2} = \frac{{75}}{2}g = 3{h_1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {iv} \right)\\
Subtract\,\left( {ii} \right)\,from\,\left( {iii} \right),\,we\,get\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{h_1} + {h_2} + {h_3}} \right) - \left( {{h_2} + {h_1}} \right) = \frac{{225}}{2}g - \frac{{100}}{2}g\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_3} = \frac{{125}}{2}g = 5{h_1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( v \right)\\
From\,\left( i \right),\left( {iv} \right)\,and\,\left( v \right),\,we\,get\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_1} = \frac{{{h_2}}}{3} = \frac{{{h_3}}}{5}\\
\,\,\,\,\,\,\,\,
\end{array}\)
\(\begin{array}{l}
\,\,\,\,\,\,\,{\rm{Distance covered}}\,by\,the\,in\,first\,5\,{\rm{second}}\,\\
\,\,\left( {i.e.t = 5\,s} \right)\,is\\
\,{h_1} = \frac{1}{2} = g{\left( 5 \right)^2} = \frac{{25}}{2}g\,\,\,\,\,\,\,...\left( i \right)\\
\,\,{\rm{Distance}}\,travelled\,by\,the\\
stone\,in\,next\,5\,\,{\rm{second}}\,\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {i.e.t = 10\,s} \right)\,is\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_1} + {h_2} = \frac{1}{2}g{\left( {10} \right)^2} = \frac{{100}}{2}g\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)\\
{\rm{Distance}}\,travelled\,by\,the\,stone\,in\,5\,{\rm{second}}\\
\left( {i.e.t = 15\,s} \right)\,\,is\\
\,\,\,\,\,\,\,\,\,\,\,\,{h_1} + {h_2} + {h_3} = \frac{1}{2}g{\left( {15} \right)^2} = \frac{{225}}{2}g\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {iii} \right)\\
Subtract\,\left( i \right)\,from\,\left( {ii} \right),\,we\,get\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{h_1} + {h_2}} \right) - {h_2} = \frac{{100}}{2}g - \frac{{25}}{2}g = \frac{{75}}{2}g\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_2} = \frac{{75}}{2}g = 3{h_1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {iv} \right)\\
Subtract\,\left( {ii} \right)\,from\,\left( {iii} \right),\,we\,get\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{h_1} + {h_2} + {h_3}} \right) - \left( {{h_2} + {h_1}} \right) = \frac{{225}}{2}g - \frac{{100}}{2}g\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_3} = \frac{{125}}{2}g = 5{h_1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( v \right)\\
From\,\left( i \right),\left( {iv} \right)\,and\,\left( v \right),\,we\,get\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_1} = \frac{{{h_2}}}{3} = \frac{{{h_3}}}{5}\\
\,\,\,\,\,\,\,\,
\end{array}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1અમુક વેગ સાથે ઉપર ફેંકેલી વસ્તુ મહત્તમ $50\,m$ ની ઊંચાઈ સુધી પહોંચે છે. તેનાથી બે ગણા દળની વસ્તુને બે ગણા વેગથી ફેંકવામાં આવે છે. તે,$..........\,m$ જેટલી મહતત્તમ ઉંચાઈ પર પહોંચશે.View Solution
- 2$\mathrm{Y}-\mathrm{Z}$ સમતલમાં ગતિ કરતી એક કીડીનું સ્થાન ( $\mathrm{S}$ મીટરમાં ) $\mathrm{S}=2 \mathrm{t}^2 \hat{j}+5 \hat{k}$ (જ્યાં $\mathrm{t}$ સેકંડમાં છે) વડે દર્શાવવામાં આવે છે. $t=1 \mathrm{~s}$ વખતે કીડીના વેગના મૂલ્ય અને દિશા _______થશે.View Solution
- 3$150\;m$ લાંબી ટ્રેન ઉત્તર દિશામાં $10\;m / s$ ના વેગથી જઇ રહી છે. એક પોપટ $5\; m / s$ ના વેગથી દક્ષિણ દિશામાં રેલના પાટાને સમાંતર ઊડી રહ્યું છે. પોપટને ટ્રેનને ક્રોસ કરવા કેટલો સમય ($sec$ માં) લાગશે?View Solution
- 4કણ $u = at$ મુજબ ગતિ કરે તો પ્રથમ $4\, sec$ માં તે કેટલું અંતર કાપશે?View Solution
- 5ટાવરની ટોચ ઉપરથી જેટલી ઝડપથી એક પદાર્થને શિરોલંબ દિશામાં ઉપર તરફ઼ પ્રક્ષિપ્ત (ફેકવામાં) કરવામાં આવે છે. તે જમીન ઉપર $t_1$ સમયમાં પહોંચે છે. જે તેને આ જ સ્થાન આગળથી આ જ ઝડપથી શિરોલંબ નીચે તરફ પ્રક્ષિપ્ત કરવામાં આવે તો તે જમીન ઉપર $\mathrm{t}_2$ સમયમાં પહોંચે છે. જો તેને ટાવરની ટોચ ઉપ૨થી મુક્ત પતન કરવામાં આવે તો તેને જમીન સુધી પહોચતા લાગતો સમય. . . . .થશે.View Solution
- 6View Solutionઅચળ પ્રવેગી ગતિ કરતાં કણ માટે સ્થાન, વેગ અને પ્રવેગનો આલેખ શેના વડે રજૂ કરવામાં આવે?
- 7એક કણ સીધી રેખા $OX$ પર ગતિ કરે છે. $t$ (સેકન્ડમાં) સમયે કણના $O$ થી અંતર $x$ (મીટરમાં) એ $x =40+12 t - t ^{3}$ વડે આપવામાં આવે છે. આ કણ સ્થિર થશે તે પહેલાં કેટલા.........$m$ અંતર કાપશે?View Solution
- 8નીચેનામાંથી ક્યા ઝડપ-સમય $(v-t)$ નો આલેખ ભૌતિક રીતે શક્ય નથી?View Solution
- 9$A $ પદાર્થ $a_1$ પ્રવેગથી સ્થિર સ્થિતિમાંથી ગતિ શરૂ કરે છે,અને $2 sec$ પછી $B$ પદાર્થ $a_2$ પ્રવેગથી સ્થિર સ્થિતિમાંથી ગતિ શરૂ કરે છે.જો બંનએ $5^{th}\, sec$ માં કાપેલ અંતર સમાન હોય તો ${a_1}:{a_2}=$View Solution
- 10$81\, m$ ઊંચાઈ પર રહેલ એક બલૂન ઉપર તરફ $12 \,m/s$ ના વેગથી ગતિ કરે છે.તેમાંથી $2\,kg$ દળના પદાર્થને મુક્ત કરવામાં આવે છે. જો $g = 10\,m/{s^2}$ હોય તો પદાર્થને જમીન પર આવતા કેટલો સમય ($sec$ માં) લાગે?View Solution
