હાઈડ્રોજન અર્ધકોષનો રિડકશન પોટેન્શિયલ ઋણ ત્યારે હોય છે, જ્યારે .........
AIEEE 2011, Medium
Download our app for free and get started
c
$H^{+}+e^{-} \longrightarrow \frac{1}{2} H_{2}$
$H^{+}+e^{-} \longrightarrow \frac{1}{2} H_{2}$
$E=E^{\circ}-\frac{0.059}{1} \log \frac{P_{H_{2}}^{1 / 2}}{\left|H^{+1}\right|}$
Now if $P_{H_{2}}=2$ atm and $\left[H^{+}\right]=1 M$
then $E=0-\frac{0.059}{1} \log \frac{2^{1 / 2}}{1}=-2$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નિકલ નાઈટ્રેટ $[Ni (NO_3)_2]$ અને ક્રોમિયમ નાઈટ્રેટ $[Cr(NO_3)_3]$ ધરાવતા બે અલગઅલગ વિદ્યુત વિભાજન કોષોમાં સમાન સંખ્યામાં વિદ્યુત પ્રવાહ પસાર કરવામાં આવે છે. જો પ્રથમ કોષમાં $0.3$ ગ્રામ નિકલજમા થાય તો ક્રોમિયમ કેટલા ............. $\mathrm{g}$ જમા થશે? ($Ni$ નો અ.ભા.$= 59$, $Cr$ નો અણુભાર $= 52$)View Solution
- 2અર્ધ-સેલ પ્રક્રિયા માટે પ્રમાણિત રીડકશન પોટેન્શિયલ આ પ્રમાણે છે:View Solution
$Zn = Z{n^{2 + }} + 2{e^ - };\,\,{E^o} = + 0.76\,V$
$Fe = F{e^{2 + }} + 2{e^ - };\,\,{E^o} = + 0.41\,V$
નીચેના કોષ પ્રક્રિયા માટે $EMF$ ......... $\mathrm{V}$ છે
$F{e^{2 + }} + Zn\, \to \,Z{n^{2 + }} + Fe$
- 3કોષનો કોષ-અચળાંક $= 0.5$ સેમી$^{-1}$ છે. $R = 50$ ઓહ્મ છે. નોર્માલિટી $= 1$ હોય, તો વીજરાસાયણિક કોષની તુલ્યવાહકતા ...... ઓહ્મ$^{-1}$ સેમી$^{2}$ ગ્રામ તુલ્ય$^{-1}$ થાય.View Solution
- 4સૂચિ $I$ સાથે સૂચિ $II$ ને જોડો.View Solution
સૂચિ $I$ (પરીવર્તન)
સૂચિ $II$ (જરૂરી ફેરાડેની સંખ્યા) $A$.$\mathrm{H}_2 \mathrm{O}$ ના $1$ મોલનું $\mathrm{O}_2$ માં $l$. $3 \mathrm{~F}$ $B$. $\mathrm{MnO}_4^{-}$ના 1 મોલનું $\mathrm{Mn}^{2+}$ મi $II$. $2 F$ $C$. પીગાળેલ $\mathrm{CaCl}_2$ માંથી Caનl $1.5$ મોલ $III$. $1F$ $D$.$\mathrm{FeO}$ ના $1$ મોલમાંથી $\mathrm{Fe}_2 \mathrm{O}_3$ $IV$. $5 \mathrm{~F}$ નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 5$298 \mathrm{~K}$. પર કોષ (image) ના વડે તેને વધારી શકાય છે.View Solution
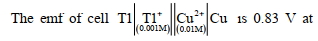
- 6$LiCl, NaCl$ અને $KCl$ ની અનંત મંદને તુલ્ય વાહકતાનો સાચો ક્રમ કયો છે?View Solution
- 7આપેલ પ્રક્રિયાView Solution
$Cu(s) + 2Ag{^+}_{(aq)} \to Cu^{+2}_{(aq)} + 2Ag(s)$
માટે સંતુલન અચળાંક $K_C = 10 \times 10^{15}$ છે, તો $298\, K$ ને $E_{cell}^o$ નું મૂલ્ય કેટલુ થશે?
[${2.303\,\frac{{RT}}{F}}$ એ $298\,K$ $=0.059\,V$]
- 8$CuSO_4$ ના જલીય દ્રાવણમાં $1 $ ફેરાડે વિદ્યુતજથ્થો પસાર કરતાં ..... મળે.View Solution
- 9View Solutionહાઈડ્રોજન અને મિથેન જેવા બળતણના દહનથી મળતી ઊર્જાનુ સીધુ જ વિધુતઊર્જામાં રૂપાંતર કરતુ સાધન .........છે.
- 10$Zn^{2+}/zn,$ $Ni^{2+} /Ni$ અને $Fe^{2+}/Fe$ ના પ્રમાણિત રિડકશન પોટેન્શિયલના મૂલ્યો અનુક્રમે $-0.76,-0.23$ અને $-0.44\, V$ છે. તો પ્રક્રિયા $X+Y^{2+} \rightarrow x^{2+} +Y$ સ્વયંભૂ ત્યારે થશે જ્યારે .......View Solution