Initial capacitance \( = \frac{{{ \in _0}A}}{d}\)
When it is half filled by a dielectric of dielectric constant \(K\), then
\(C_{1}=\frac{K \varepsilon_{0} A}{d / 2}=2 K \frac{\varepsilon_{0} A}{d}\)
and \(C_{2}=\frac{\varepsilon_{0} A}{d / 2}=\frac{2 \varepsilon_{0} A}{d}\)
\(\therefore \frac{1}{{{C^\prime }}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} = \frac{d}{{2{\varepsilon _0}A}}\left( {\frac{1}{K} + 1} \right)\)
\( = \frac{d}{{2{\varepsilon _0}A}}\left( {\frac{1}{5} + 1} \right) = \frac{6}{{10}}\frac{d}{{{\varepsilon _0}A}}\)
\(C = \frac{{5{\varepsilon _0}A}}{{3d}}\)
Hence, \(\%\) increase in capacitance
\({ = \left( {\frac{{\frac{5}{3}\frac{{{\varepsilon _0}A}}{d} - \frac{{{\varepsilon _0}A}}{d}}}{{\frac{{{\varepsilon _0}A}}{d}}}} \right) \times 100}\)
\({ = \left( {\frac{5}{3} - 1} \right) \times 100 = \frac{2}{3} \times 100 = 66.6\% }\)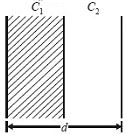
Download our appand get started for free
Similar Questions
- 1$R$ ત્રિજ્યાની એક પાતળી સુવાહક કવચ પરનો વિદ્યુતભાર $q$ છે. બીજો $Q$ વિદ્યુતભાર કવચના કેન્દ્ર આગળ મૂકેલો છે. કવચના કેન્દ્રથી $R/2$ અંતરે $P$ બિંદુ આગળ વિદ્યુત શાસ્ત્રનું વિદ્યુત સ્થિતિમાન ........ છે.View Solution
- 2$10\ \mu F$ મૂલ્ય ધરાવતા બે કેપેસિટરોના સમાંતર જોડાણને $200 \,volt\, dc$ થી વિદ્યુતભારીત કરવામાં આવે તો જૂલમાં સંગ્રહિત ઊર્જા કેટલી હશે ?View Solution
- 3પ્રોટોનનું દળ $1.67 \times 10^{-27} kg$ અને તેનો ચાર્જ $+1.6 \times 10^{-19} C$ છે. દસ લાખ વોલ્ટના વિદ્યુત સ્થિતિમાનનાં તફાવતે જો તેને પ્રવેગીત કરવામાં આવે તો તેની ગતિઊર્જા $\dots\dots J$ થશે.View Solution
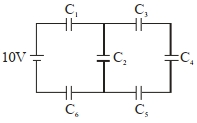
- 4આપેલા પરિપથ માટે $C _1=2\,\mu F , C _2=0.2\,\mu F$, $C _3=2\,\mu F , C _4=4\,\mu F$, $C _5=2 \,\mu F , C _6=2\, \mu F$, સંગ્રાહક $C _4$ ના સંગ્રહ થતો વિજભાર ........... $\mu C$ છે.View Solution
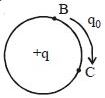
- 5$R$ ત્રિજયા ધરાવતા વર્તુળના કેન્દ્ર પર $+ q$ વિદ્યુતભાર મૂકેલો છે. $q_0$ વિદ્યુતભારને $B$ થી $C$ લઈ જવા માટે થતું કાર્ય કેવું હશે?View Solution
- 6$x-y$ અક્ષોની પ્રણાલીનાં ઉગમ બિંદુ એક $10\,\mu C$ જેટલો ચાર્જ મુકવામાં આવ્યો છે. $(0, a)$ પર $(a, 0)$ બિંદુઓ વચ્ચે કેટલો વિદ્યુત સ્થિતિમાનનો ફરક જોવાં મળશે?View Solution
- 7બે પ્લેટો એકબીજાથી $20\, cm$ દૂર છે. તેમની વચ્ચે વિદ્યુુત સ્થિતિમાનનો તફાવત $10\, volt$ છે, તો બે પ્લેટો વચ્ચે વિદ્યુતક્ષેત્ર ......$Vm^{-1}$View Solution
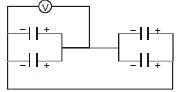
- 8$25\,\mu \,F$ ના ચાર કેપેસીટરને આકૃતિમાં દર્શાવ્યા મુજબ જોડેલા છે. જો $dc$ વોલ્ટમીટરનું અવલોકન $200\,V$ હોય તો કેપેસીટરની દરેક પ્લેટ પરનો વિદ્યુતભાર કેટલો હશે?View Solution
- 9જ્યારે સમાંતર પ્લેટ કેપેસીટરની બે પ્લેટો વચ્ચેનું અંતર $6\, cm$ હોય ત્યારે તેનું કેપેસીટન્સ $15\ \mu F$ છે પ્લેટો વચ્ચેનું અંતર $2\ cm$ સુધી ઘટાડવામાં આવે તો સમાંતર પ્લેટ કેપેસીટરનું કેપેસીટન્સ....$\mu F$View Solution
- 10$R$ અને $2 R$ ત્રિજ્યા ધરાવતા બે ધાતુના ગોળાની પૃષ્ઠવિજભાર ઘનતા $\sigma$ સમાન છે.તે બંનેને સંપર્કમાં લાવવામાં આવે છે અને પછી અલગ કરવામાં આવે છે.તો તેના પર નવી પૃષ્ઠવિજભાર ઘનતા કેટલી થશે?View Solution
