$i=10\, A$ પ્રવાહધારિત ખંડ $d l=d x \hat{l}$ (જ્યાં , $d x=1$ સેમી )ને ઉદગમબિંદુએ મૂકેલો છે, તો $Y$ - અક્ષ પર $0.5\;m$ અંતરે ચુંબકીય ક્ષેત્ર કેટલું થાય?
AIIMS 2018, Diffcult
Download our app for free and get started
b
Here, \(d l=d x=1 cm =10^{-2} m\),
Here, \(d l=d x=1 cm =10^{-2} m\),
\(i=10 A , r=0.5 m\)
\(\therefore d B=\frac{\mu_{0}}{4 \pi} \cdot \frac{i(d l \times r)}{r^{3}}\)
\(=\frac{\mu_{0}}{4 \pi} \cdot \frac{i d l}{r^{2}}(\hat{\imath} \times \hat{j})=\frac{\mu_{0}}{4 \pi} \cdot \frac{i d l}{r^{2}} \hat{k}\)
\(=\frac{10^{-7} \times 10 \times 10^{-2} \sin 90^{\circ}}{(0.5)^{2}} \hat{k}\)
\(=4 \times 10^{-8} \hat{k} T\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એકસમાન ચુંબકીયક્ષેત્ર $\overrightarrow B $ માં એક વિજભારિત કણ $v$ વેગથી ગતિ કરે છે. કણ દ્વારા અનુભવાતું ચુંબકીય બળ કેટલું હશે?View Solution
- 2સમકેન્દ્રિય કેબલમાં અંદરના તારની ત્રિજ્યા $a$ છે જે અંદરની અને બહારની ત્રિજ્યા ${b}$ અને $c$ તારથી ઘેરાયેલ છે. અંદરના તારમાં વિદ્યુતપ્રવાહ સમગ્ર આડછેડ પર સમાન રીતે વિતરિત થયેલ છે. બહારના તારમાં સમાન રીતે વિતરિત થયેલ તેટલો જ પ્રવાહ પરતું વિરુદ્ધ દિશામાં વહન પામે છે. તેમની અક્ષથી $x$ અંતરે ચુંબકીયક્ષેત્રનો ગુણોત્તર જ્યારે$(i)$ ${x}<{a}$ અને $(ii)$ ${a}<{x}<{b}$ હોય ત્યારે કેટલો થાય?View Solution
- 3$20\, turns/cm$ ધરાવતા સોલેનોઇડમાં $20\, millitesla$ ચુંબકીયક્ષેત્ર ઉત્પન્ન કરવા માટે કેટલો પ્રવાહ પસાર કરવો પડે?.......$A$ $\left( {\frac{{{\mu _0}}}{{4\pi }} = {{10}^{ - 7}}\,Tesla{\rm{ - }}metre\,/\,ampere} \right)$View Solution
- 4એક પ્રોટોન અને એક $\alpha-$કણ (તેમનાં દ્રવ્યમાનનો ગુણોત્તર $1:4$ અને વિધુતભારનો ગુણોત્તર$1: 2$) સ્થિર સ્થિતિમાંથી $V$ વિજસ્થિતિમાનના તફાવતથી પ્રવેગીત કરવામાં આવે છે. જો તેમની ગતિઓને લંબ એકસમાન ચુંબકીય ક્ષેત્ર $(B) $ પ્રસ્થાપિત કરવામાં આવે, તો તેઓ વડે કપાતા વર્તુળાકાર પથની ત્રિજ્યાઓનો ગુણોત્તર $r_p : r_{\alpha }$ કેટલો થશે?View Solution
- 5$n$ આંટાવાળી અને $2l$ બાજુવાળી ચોરસફ્રેમના કેન્દ્ર પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 6અચળ વેગ સાથે ગતિ કરતો પ્રોટોન અવકાશના વિસ્તારમાંથી તેના વેગમાં ફેરફાર થયા વગર, પસાર થાય છે. જો $E$ અને $B$ નીચેનામાંથી ક્યું હોઈ શકે ?View Solution
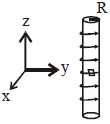
- 7$R$ ત્રિજ્યા ધરાવતા લાંબા સોલેનોઈડની અંદર અક્ષ પર એક ઇલેક્ટ્રોન ગન મૂકવામાં આવેલ છે. સોલેનોઈડમાં એકમ લંબાઈ દીઠ આંટાની સંખ્યા $n$ અને વહેતો પ્રવાહ $I$ છે.ઇલેક્ટ્રોન ગન સોલેનોઈડમાં ત્રિજયવર્તી દિશામાં $v$ વેગથી ઇલેક્ટ્રોન છોડે છે. જો ઇલેક્ટ્રોન સોલેનોઈડની સપાટી પર પહોચે નહીં તે માટે તેનો મહત્તમ વેગ $v$ કેટલો હોવો જોઈએ?View Solution
- 8$0.5\, mm$ વ્યાસવાળા સુરેખ તારમાંથી $1\, A$ વિદ્યુતપ્રવાહ વહે છે તેને $1\,mm$ વ્યાસવાળો $1\, A$ વિદ્યુતપ્રવાહનું વહન કરતાં બીજા તાર વડે બદલવામાં આવે, તો ખૂબ દૂર આવેલા બિંદુ પાસે ચુંબકીય ક્ષેત્ર .....View Solution
- 9બંનેમાંથી સમાન પ્રવાહ પસાર થતો હોય તેવા બે ગૂંચળાઓ $X$ અને $Y$ ના કેન્દ્ર આગળ અનુક્રમે ચુંબકીય ક્ષેત્રો $B_X$ અને $B_Y$ છે. જે $X$ ગૂંચળામાં આંટાની સંખ્યા $200$ અને ત્રિજ્યા $20\,cm$ અને $Y$ ગુંચળામાં આંટાની સંખ્યા $400$ અને ત્રિજ્યા $20\,cm$ છે, તો $B_X$ અને $B_Y$ નો ગુણોતર થશે.View Solution
- 10View Solutionવિદ્યુત પ્રવાહ ધારીત કોઇલમાં ઉર્જા કયા સ્વરૂપે સંગ્રહ થાય છે?