જો $\overrightarrow{ F }=3 \hat{i}+4 \hat{j}-2 \hat{k}$ બળ એ $2 \hat{i}+\hat{j}+2 \hat{k}$ સ્થાન સદીશ ધરાવતા કણ ઉપર લાગતો હોય, તો ઊગમબિંદુને અનુલક્ષીને ટોર્ક............હશે
JEE MAIN 2022, Easy
Download our app for free and get started
b
\(\vec{\tau}=\vec{r} \times \vec{F}\)
\(\vec{\tau}=\vec{r} \times \vec{F}\)
\(=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 2 \\ 3 & 4 & -2\end{array}\right|\)
\(=\hat{\hat{i}}(-2-8)-\hat{ j }(-4-6)+\hat{ k }(8-3)\)
\(=-10 \hat{ i }+10 \hat{ j }+5 \hat{ k }\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$m_1 = fM$ અને $m_2 = (1 -f)\,M\,(f < 1 )$ દળના બે સૂક્ષ્મદળો બાહ્ય અવકાશમાં (બીજી કોઈ વસ્તુની ગુરુત્વઅસરથી દૂર) એકબીજાથી $R$ અંતરે છે. તે બંને તેમના દ્રવ્યમાન કેન્દ્ર ને અનુલક્ષીને વર્તુળાકાર કક્ષા માં $m_1$ એ $\omega _1$ અને $m_2$ એ $\omega _2$ કોણીય વેગથી ગતિ કરે છે.તો આ કિસ્સામાં કોણીય વેગ .....View Solution
- 2ધન ગોળા $A$ અક્ષ $PQ$ ને અનુલક્ષીને ચાકગતિ કરે છે. જો ગોળાની ત્રિજ્યા $5\,cm$ હોય, તો તેની અક્ષ $PQ$ ને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા $\sqrt{x}\; cm$ થશે. અહી $x$ નું મૂલ્ય $........$ હશે.View Solution
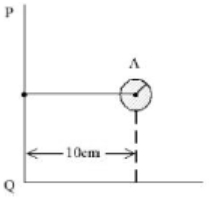
- 3View Solutionએક કણ નિયમિત વર્તુળાકાર ગતિ માંથી પસાર થાય છે. વર્તુળના સમતલ માં ક્યા બિંદુ એ કણનો કોણીય વેગમાન સંરક્ષિત (અચળ) હશે ?
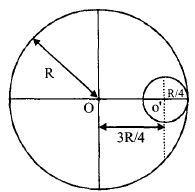
- 4આકૃતિમાં દર્શાવ્યા મુજબ $M$ દળ અને $R$ ત્રિજ્યાની એક પાતળી નિયમિત તકતીમાં $\frac{R}{4}$ ત્રિજ્યાનો વર્તુળાકાર છેદ પાડેલો છે. તો બાકી રહેલા ભાગ ની તેના $O$ માથી પસાર થતી અક્ષને અનુલક્ષીને તકતીના સમતલને લંબ જડત્વની ચાકમાત્રા શું થાય?View Solution
- 5$R$ ત્રિજ્યા અને $9M$ દળની વર્તુળાકાર તકતીમાંથી સમકેન્દ્રિય રહેલ $\frac{R}{3}$ ત્રિજ્યા અને $M$ દળની નાની તકતીને દૂર કરવામાં આવે છે. બાકી રહેલી તકતીની તકતીના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 6$l$ લંબાઈના ચોરસના ચારે ખૂણા પર $m $ દળના પદાર્થ મૂકેલા છે.તો ચોરસના સમતલને લંબ અને તેના કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજયા કેટલી થાય?View Solution
- 7સમાન દળ અને સમાન જાડાઇની તકતીની ઘનતાનો ગુણોત્તર $1:3$ છે.તો તેની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રાનો ગુણોત્તર કેટલો થાય?View Solution
- 8View Solutionપદાર્થના બધા જ કણો વર્તૂળાકાર પથમાં ગતિ કરે છે. જ્યારે તેની ભ્રમણ અક્ષ.........
- 9ટ્રકના ટાયરની કોણીય ઝડપ $900\, rpm$ થી $2460\, rpm$ થતાં $26$ સેકન્ડ લાગે છે. તો આ સમય દરમિયાન ટાયર દ્વારા થતાં પરિભ્રમણ કેટલા હશે? (પ્રવેગ અચળ ધારો)View Solution
- 10સમાન દળ ' $M$ અને ' $2 R$ ' જેટલી ત્રિજ્યા ધરાવતા ચાર વસ્તુઆની ઝડત્વની ચાકમાત્રા $(M.I.)$ નીચે મુજબ છેView Solution
$I _{1}=$ તેના વ્યાસને અનુલક્ષીને ધન ગોળાની $M.I.$
$I _{2}=$ તેની અક્ષને અનુલક્ષીને ધન નળાકારની $M.I.$
$I _{3}=$ તેના વ્યાસને અનુલક્ષીને ધન તક્તિની $M.I.$
$I _{4}=$ તેના વ્યાસને અનુલક્ષીને પાતળી વર્તુળાકાર રીંગની $M.I.$
જો $2\left( I _{2}+ I _{3}\right)+ I _{4}=x \cdot I _{1}$ હોય તો $x$ નું મૂલ્ય ........થશે.