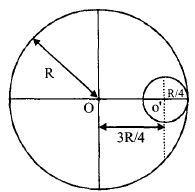
આકૃતિમાં દર્શાવ્યા મુજબ $M$ દળ અને $R$ ત્રિજ્યાની એક પાતળી નિયમિત તકતીમાં $\frac{R}{4}$ ત્રિજ્યાનો વર્તુળાકાર છેદ પાડેલો છે. તો બાકી રહેલા ભાગ ની તેના $O$ માથી પસાર થતી અક્ષને અનુલક્ષીને તકતીના સમતલને લંબ જડત્વની ચાકમાત્રા શું થાય?

JEE MAIN 2017, Diffcult
b
Moment of Inertia of complete disc about
Moment of Inertia of complete disc about
\('O'\) point \({I_{total}} = \frac{{M{R^2}}}{2}\)
Radius of removed disc \(= R/4\)
Mass of removed disc \(= M/16\) [As \(M\) \( \propto \) \({{R^2}}\)]
\(M.I.\) of removed disc about its own axis \((O')\)
\( = \frac{1}{2}\frac{M}{{16}}{\left( {\frac{R}{4}} \right)^2} = \frac{{M{R^2}}}{{512}}\)
\(M.I\) of removed disc about \(O\)
\(\begin{array}{l}
{I_{remo\,ved\,disc\,}} = {I_{cm}} + m{x^2}\\
= \frac{{M{R^2}}}{{512}} + \frac{M}{{16}}{\left( {\frac{{3R}}{4}} \right)^2} = \frac{{19\,M{R^2}}}{{512}}
\end{array}\)
\(M.I.\) of remaining disc
\({I_{remaining}} = \frac{{M{R^2}}}{2} - \frac{{19}}{{512}}M{R^2} = \frac{{237}}{{512}}M{R^2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નિયમિત વર્તૂળાકાર ગતિ કરવા વ્હીલ પર અચળ ટૉર્ક લગાડતાં તેનું કોણીય વેગમાન $4$ સેકન્ડમાં $A_0$ થી $4A_0$ બદલાઈ થાય છે. આ ટૉર્કનું મૂલ્ય .......View Solution
- 2$m$ અને $M$ $(M>m)$ ના દળોનું દ્રવ્યમાન કેન્દ્રView Solution
- 3ત્રણ સમાન પાતળી લાકડી જેની લંબાઈ $l$ અને દળ $M$ છે તેને જોડીને $H$ અક્ષર બનાવવામાં આવે તો તંત્ર ની $H $ ની કોઈ એક બાજુને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
- 4$1.5\ m$ ત્રિજ્યાનું વ્હીલ $10\ rad/s^2$ ના અચળ પ્રવેગથી ચાકગતિ કરે છે તેની પ્રારંભિક કોણીય ઝડપ $\left( {\frac{{60}}{\pi }} \right)\,\,rpm.$ છે તેની કોણીય ઝડપ અને કોણીય સ્થાનાંતર $ t = 2.0\ sec$ એ ........ $rad$ થશે ?View Solution
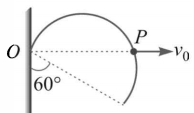
- 5એક પાતળી પણ દઢ અર્ધવતુળ વાયરની ફેમ જેની ત્રિજ્યા $r$ છે તેને $O$ આગળ લટકાવેલ છે અને તે પોતાના જ લંબગત સમતલ પર ફરે છે. એક હળવા $Peg$ $P$ ને $O$ થી શરૂ કરી અચળ વેગ $v _0$ થી આડી દિશામાં ગતિ કરે છે, અને ફ્રેમને ઊંચે લઈ જવાય છે. જ્યારે તે લંબ જોડે $60^{\circ}$ નો ખૂણો બનાવે ત્યારે આ ફ્રેમનો કોણીય વેગ શોધો.View Solution
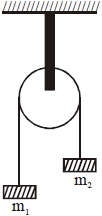
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે એક પાતળા ચક્રની ત્રિજ્યા $R$ અને જડત્વની ચાકમાત્રા $I$ છે જે પોતાના દ્રવ્યમાન કેન્દ્રને અનુલક્ષીને મુક્ત રીતે ફરી શકે છે.તેના પર બે દળ $\mathrm{m}_{1}$ અને $\mathrm{m}_{2}\left(\mathrm{m}_{1}>\mathrm{m}_{2}\right)$ ને દળરહિત દોરી દ્વારા લટકવેળા છે.જ્યારે તંત્રને સ્થિર સ્થિતિમાંથી મુક્ત કરવામાં આવે ત્યારે $\mathrm{m}_{1}$ દળ નીચે તરફ $h$ અંતર સુધી ગતિ કરે ત્યારે ચક્રની કોણીય ઝડપ કેટલી થશે?View Solution
- 7જો કુલ ગતિ ઊર્જાનો $50\%$ ચાક ગતિ ઊર્જા હોય તો તે પદાર્થ .......... છે.View Solution
- 8એક $\theta $ કોણવાળા ઢાળ પરથી સરકયા સિવાય ગબડીને અને ગબડયા સિવાય સરકીને નીચે આવતાં ઘન ગોળા (દળ $m$ અને ત્રિજયા $ R$) ના પ્રવેગનો ગુણોત્તર કેટલો થાય?View Solution
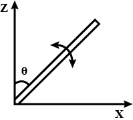
- 9$M$ દળના અને $l$ લંબાઈના એક સ્લેન્ડર એકસમાન સળીયાને એક છેડાથી ધરીમાં એ રીતે જોડેલ છે કે જેથી તે ઊર્ધ્વતલમાં ભ્રમણ કરી શકે (આકૃતિ જુઓ). ધરી પર અવગણ્ય ધર્ષણ છે. મુક્ત છેડાને ઊર્ધ્વ દિશામાં ધરીની ઉપરની તરફ રાખેલ છે અને ત્યારબાદ તેને મુક્ત કરવામાં આવે છે. સળિયાનો કોણીય પ્રવેગ જ્યારે તે ઊર્ધ્વ સાથે $\theta$ ખુણો બનાવે ત્યારે કેટલો હશે?View Solution
- 10$1.5 \,m$ લાંબા એક સળિયાના $A$ અને $B$ છેડાઓ પર અનુક્રમે $20 \,N$ અને $30 N$ ના એેક જ જેવા સમાંતર બળો લગાડવામાં આવે છે. તો આ બળોનું પરિણામી બળ ક્યા બિંદુ પર લાગતું હશે?View Solution
