જો શંકુઆકારનાં લોલકની દોરી સમક્ષિતિજ સાથે $\theta$ કોણ બનાવે છે, તો પછી તેના આવર્તકાળનો વર્ગ કોના સમપ્રમાણમાં હશે?
Medium
Download our app for free and get started
a
(a)
(a)
For conical pendulum we know that
\(T=2 \pi \sqrt{\frac{l \cos \theta}{g}}\)
where \(\theta\) is the angle from vertical but in question \(\theta\) is given from horizontal hence
\(T=2 \pi \sqrt{\frac{l \sin \theta}{g}}\)
\(T^2 \propto \sin \theta\)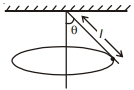
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જમીન પર રહેલા માણસને ફૂડ પેકેટ આપવા માટે એક હેલિકોપ્ટર $h$ ઊંચાઈએ સમક્ષિતિજ દિશામાં $v$ વેગથી ગતિ કરે છે.જ્યારે ફૂડ પેકેટ મૂકવામાં આવે હેલિકોપ્ટર માણસથી કેટલા અંતરે હોવું જોઈએ?View Solution
- 2એક પૈડું વિરામ સ્થિતિમાંથી નિયમિત રીતે પ્રવેગીત થાય છે અને પ્રથમ સેકન્ડમાં $5 \;rad$ જેટલું ભ્રમણ કરે છે. બીજી સેકન્ડમાં કપાયેલ કોણ.....$rad$ હશે.View Solution
- 3ચોક્કસ સમયે વર્તુળાકાર ગતિ કરતા કણના વેગના અને પ્રવેગ સદિશો અનુક્રમે $\vec{v}=2 \hat{i} m / s$ અને $\vec{a}=2 \hat{i}+4 \hat{j} m / s^2$ છે.તો વર્તુળની ત્રિજ્યા $ ........\,m$View Solution
- 4$20\, km$ ત્રિજયા ધરાવતો ગ્રહ $1$ પરિભ્રમણ/સેકન્ડના દરથી ફરે છે,તો તેના વિષુવવૃત પર રહેલા પદાર્થનો પ્રવેગ કેટલો હશે?View Solution
- 5એક એરક્રાફ્ટ $150\, m/s$ ની ઝડપથી તેના પાંખિયા ને $12^o$ ના ખૂણે રાખીને સમક્ષિતિજ વર્તુળાકાર લૂપ રચે છે. તો વર્તુળાકાર લૂપ ની ત્રિજ્યા .......... $km$ થશે.View Solution
$(g = 10\, m/s^2 \; and\; \tan 12^o = 0.2125)$
- 6$\alpha= 30^o$ ખૂણો ધરાવતા ઢાળ પર સમક્ષિતિજ સાથે $\beta = 60^o$ ના ખૂણે $21 \,m/sec$ ના વેગથી ગોળી છોડતાં અવધિ ....... $m$ મળે .View Solution
- 7એક તરવૈયાને બિંદુ $A$ થી બિંદુ $B$ સુધી નદી પસાર કરવી છે. $AB$ રેખા પાણીના વાહન સાથે $30^{\circ}$ નો ખૂણો બનાવે છે. તરવૈયાના તરવાના વેગનું મૂલ્ય નદી (પાણી) જેટલું જ છે. ${AB}$ રેખા સાથેનો કોણ $\theta$ કે જેથી તરવૈયો બિંદુ $B$ પર પહોચે તે $^{\circ}$ માં કેટલો હશે?View Solution
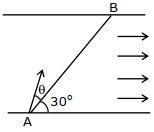
- 8View Solutionઅચળ મુલ્યનું બળ બે કણની ગતિની દિશાને લંબ લાગે છે, તો પછી તેની
- 9જો પ્રક્ષિપ્ત ગતિમાં સમક્ષિતિજ દિશામાં પ્રારંભિક વેગ એ એકમ સદિશ $\hat{i}$, અને ગતિપથનું સમીકરણ $y=5 x(1-x) $ છે.તો પ્રારંભિક વેગનો $y-$ઘટક $.......\hat{j}$ હશે.($g=10\,m / s ^{2}$ ) લો.View Solution
- 10$4 \,m$ ત્રિજયાનું પૈડું $2 \,sec$ માં એક પરિભ્રમણ પુરું કરે છે. તો સાઇકલનો પ્રવેગ શોધો.View Solution