જયારે પંખો ચાલુ કરવામાં આવે છે ત્યારે પ્રથમ $3\, sec$ માં $10 $ પરિભ્રમણ કરે છે. પછી બીજી $3\, sec$ માં કેટલા પરિભ્રમણ કરશે $?$ (અહીં અચળ કોણીય પ્રવેગ લાગે છે.)
Medium
c
In first three seconds, angle rotated \(\theta=2 \pi \times 10 \mathrm{rad}\)
In first three seconds, angle rotated \(\theta=2 \pi \times 10 \mathrm{rad}\)
Using, \(\theta=\omega_{0} t+\frac{1}{2} \alpha t^{2}\)
\(\therefore 2 \pi \times 10=0+\frac{1}{2} \alpha \times 3^{2}=\frac{9}{2} \alpha \ldots(i)\)
For the rotation of fan in next three second, the total time of revolutions
\(=\)\(3+3=6 s\)
Let total number of revolutions \(=N\)
Then angle of revolutions, \(\theta^{\prime}=2 \pi \mathrm{N}\) rad
\(\therefore 2 \pi N=0+\frac{1}{2} \alpha \times 6^{2}=18 \alpha\) \(...(ii)\)
Dividing \((ii)\) by \((i),\) we get
\(N=40\)
No. of revolutions in last three seconds
\(=40-10=30\) revolutions
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પાતળો તાર જેની લંબાઈ $l$ અને દળ $M$ છે તેને વાળીને અડધું વર્તુળ બનાવવામાં આવે છે. તો તારના છેડાઓ પાસેથી પસાર થતી અક્ષ ને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય ?View Solution
- 2$100\,kg$ દળનો માણસ એ $200\,kg$ ના પ્લેટફોર્મ પર ઉભો છે. જે સૂવાળી બરફની સપાટી પર છે. જો માણસ પ્લેટફોર્મ પર $30\,m / s$ ના વેગથી ગતિ કરે છે, તો $..........m/s$ વેગથી પ્લેટફોર્મ એ બરફની સાપેક્ષમાં પાછુ ખસશે.View Solution
- 3એક ઘન ગોળો ગબડતી ગતિમાં છે.ગબડતિ ગતિ (લોટણ ગતિ) માં પદાર્થ સ્થાનાંતરીત ગતિઊર્જા $(K_t) $ અને ભ્રમણીય ગતિઊર્જા $(K_r)$ એક સાથે ધરાવે છે.આ ગોળા માટે $ K_t: (K_t+ K_r)$ નો ગુણોત્તર છે.View Solution
- 4View Solutionએક નક્કર ગોળો એક ખરબચડા ઢોળાવ ઉપર ફેંકવામાં આવે છે. ગોળો સરક્યાં વિના ગબડે છે અને અંતે સરક્યાં વિના નીચે આવે છે. રોલિંગ ઘર્ષણની ઉપરની અને નીચેની ગતિની દિશા અનુક્રમે શું છે?
- 5પાતળી ચોરસ પ્લેટ $ ABCD $ ની જાડાઈ નિયમિત છે. તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
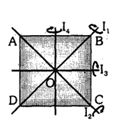
- 6આકૃતિમાં નિયમિત ચોરસ પ્લેટ દર્શાવેલી છે. જેના ખૂણા પરથી ચાર સમાન ચોરસ દૂર કરવામાં આવ્યા છે. ચોરસ $1$ અને $2$ ને દૂર કરતાં $ C.M.$ ક્યાં મળશે ?View Solution
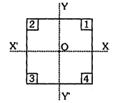
- 7$R$ જેટલી ત્રિજ્યા અને $M$ દળ ધરાવતા એક સમાંગી ઘન નળાકારીય રોલરને એક ક્રિકેટ પીચ પર સમક્ષિતિજ બળ $F$ ની મદદથી ખેંચવામાં આવે છે. રોલર સરક્યા સિવાય ગબડે છે તેમ ધારતા, નળાકારનો કોણીય પ્રવેગ કેટલો હશેView Solution
- 8View Solutionસુરેખ સપાટી પર કોઈ તકતી સરક્યાં વગર ગબડે છે. તો રેખીય ગતિઉર્જા નો કુલ ગતિઉર્જા સાથેનો ગુણોત્તર શું મળે?
- 9$M$ દળ અને $ R$ ત્રિજ્યાની ગોળાની જડત્વની ચાકમાત્રા $ I$ છે. $M$ અચળ રાખીને $ I $ વિરૂદ્ધ $R$ નો આલેખ કયો મળે?View Solution
- 10$R $ ત્રિજ્યાની રિંગની રીમ પર સ્પર્શીંય બળ $ F $ લાગવાના કારણે તે $\theta$ કોણે ફરે છે. બળ દ્વારા થતું કાર્ય કેટલું થશે ?View Solution
