એક ઘન ગોળો ગબડતી ગતિમાં છે.ગબડતિ ગતિ (લોટણ ગતિ) માં પદાર્થ સ્થાનાંતરીત ગતિઊર્જા $(K_t) $ અને ભ્રમણીય ગતિઊર્જા $(K_r)$ એક સાથે ધરાવે છે.આ ગોળા માટે $ K_t: (K_t+ K_r)$ નો ગુણોત્તર છે.
NEET 2018,AIPMT 1991, Medium
b
Translational kinetic energy, \({K_t} = \frac{1}{2}m{v^2}\)
Translational kinetic energy, \({K_t} = \frac{1}{2}m{v^2}\)
Rotational kinetic energy, \({K_r} = \frac{1}{2}I{\omega ^2}\)
\(\begin{array}{ccccc}
\therefore \,{K_t} + {K_r} = \frac{1}{2}m{v^2} + \frac{1}{2}I{\omega ^2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}m{v^2} + \frac{1}{2}\left( {\frac{2}{5}m{r^2}} \right){\left( {\frac{v}{r}} \right)^2}\\
\therefore \,{K_t} + {k_r} = \frac{7}{{10}}m{v^2}\,\,\,\,\,\,\left[ {I = \frac{2}{5}m{r^2}\left( {for\,sphere} \right)} \right]\\
So,\,\frac{{{K_t}}}{{{K_t} + {K_r}}} = \frac{5}{7}
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક વજનદાર તકતી અચળ કોણીય વેગ $\omega$ થી તકતીના સમતલને લંબ અને કેન્દ્રથી પસાર થતી અક્ષને અનુલક્ષીને ફરે છે. તેનું કોણીય વેગમાન $L$ છે. પ્લાસ્ટિકનો એક ટુકડો તકતી પર લંબરૂપે પડે છે અને તેના પર ચોંટી જાય છે તો નીચેનામથી શું અચળ હશે ?View Solution
- 2$5\,kg$નું એક બાળક ચકડોળમાં ફરે છે જે $3.14\,s$ માં $1$ પરિભ્રમણ પૂર્ણ કરે છે. ચકડોળની ત્રિજ્યા $2\,m$ છે. બાળક પર લાગતું કેન્દ્રત્યાગી બળ $.......\,N$ હશેView Solution
- 3એક પદાર્થ માત્ર કોણીય ગતિ કરે છે જો કણ નો રેખીય વેગ $v$ અને તે $x$-અક્ષ થી $r$ અંતરે $\omega $ કોણીય વેગ થી ફરતો હોય $\omega = \frac{v}{r}$ હોય તો પદાર્થ માટે શું સાચું છે ?View Solution
- 4$0.01\ kg $ દળનો કણનો સ્થાન સદિશ $\overline r \,\, = \,\,\,(10\hat i\,\,\, + \,\,\,6\hat j\,)$ મીટર છે અને તે $5\,\hat i\,\,m/s$ વેગથી ગતિ કરે છે તો તેનું ઊગમબિંદુ આસપાસ કોણીય વેગમાન ......... $\hat k\,\,J/\sec $ ગણો.View Solution
- 5$m_1$ અને $m_2$ $(m_1 > m_2)$ દળના બે કણો સ્થિર સ્થિતિમાથી શરૂ કરીને એકબીજા તરફ આકર્ષીબળ ના વ્યસ્ત વર્ગના નિયમ મુજબ ગતિ કરે છે. આ તંત્ર માટે દ્રવ્યમાન $(CM)$ કેન્દ્ર માટે નીચેનામાથી સાચું વિધાન પસંદ કરો.View Solution
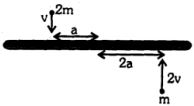
- 6$8\ m$ દળ અને $ 6\ a $ લંબાઇનો નિયમિત સળિયો સમક્ષિતિજ ટેબલ પર મૂકેલો છે બે બિંદુવત દળ $ m$ અને $2\ m$ અનુક્રમે $2v$ અને $v$ ઝડપથી ગતિ કરે છે અને સળિયાને અથડાઇને અથડામણ બાદ તેની સાથે ચોટી જાય છે.અથડામણ બાદ સળિયાના દ્રવ્યમાન કેન્દ્રની ઝડપ ગણો.View Solution
- 7એક પૈડું સ્થિર સ્થિતિમાંથી $6\ sec$ માં $540\ rpm $ ની કોણીય ઝડપ પ્રાપ્ત કરે,તો તેનો કોણીય પ્રવેગ કેટલો થાય?View Solution
- 8$500\,g$ દળ અને $5\,cm$ ત્રિજ્યા ધરાવતા એક ધન ગોળો તેના એક વ્યાસને અનુલક્ષીને $10\,rad\,s ^{-1}$ ની કોણીય ઝડપથી ભ્રમણ કરે છે. જો ગોળાને તેના સ્પર્શકને અનુલક્ષીને જડત્વની ચાકમાત્રા તેના વ્યાસને સાપેક્ષ તેના કોણીય વેગમાન કરતા $x \times 10^{-2}$ ગણી છે. $x$ નું મૂલ્ય ...... થશે.View Solution
- 9$3\; kg $ નો ઘન નળાકાર $4 \;m/s $ ના વેગથી સમક્ષિતિજ સપાટી પર ગબડે છે. તે $200\; N/m $ બળઅચળાંક ધરાવતી સમક્ષિતિજ સ્પિંગ્ર સાથે અથડાય છે. સ્પિંગનું મહતમ સંકોચન ($m$ માં) કેટલું થાય?View Solution
- 10જો $\mathop {\rm{F}}\limits^ \to \, = \left( {\,4\hat i- 10\hat j\,} \right)$ અને $\mathop r\limits^ \to = \left( {\,5\hat i- 3\hat j\,} \right)$ હોય તો $\left( {\,\mathop \tau \limits^ \to = \mathop r\limits^ \to \times \mathop F\limits^ \to } \right)$ ની ગણતરી ... થાયView Solution
