જ્યારે ઉપગ્રહ પૃથ્વીની સપાટીથી $h$ ઊંચાઈએ વર્તુળાકાર કક્ષામાં પરિભ્રમણ કરતો હોય, ત્યારે તેનું કોણીય વેગમાન $L$ છે. જો ઉપગ્રહનું પૃથ્વીના કેન્દ્રથી અંતર તેના મૂળ મૂલ્ય કરતા આઠ ગણું કરવામાં આવે, તો નવું કોણીય વેગમાન $........\,L$ થાય.
JEE MAIN 2023, Medium
d
\(L = mvr\)
\(L = mvr\)
\(v =\sqrt{\frac{ GM _{\odot}}{ r }}\)
\(L=m \sqrt{\frac{ GM _e}{ r }} \cdot r\)
\(L \propto r ^{\frac{1}{2}}\)
Now distance from centre is increased by \(8\) times.
So new distance from centre \(=r+8 r=9 r\)
Now angular momentum \(L^{\prime} \propto(9 r )^{1 / 2}\)
So new distance from centre \(=r+8 r=9 r\)
Now angular momentum \(L^{\prime} \propto(9 r)^{1 / 2}\)
\(\frac{L}{L^{\prime}}=\frac{ r ^{1 / 2}}{(9 r )^{1 / 2}}=\frac{1}{3}\)
\(L^{\prime}=3 L\)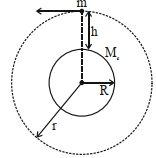
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વીની સપાટીથી $R$ ઊંચાઇ પર રહેલા ઉપગ્રહનો આવર્તકાળ કેટલો થાય?View Solution
- 2પદાર્થને એક ગ્રહ પરથી એવી રીતે ફેક્વામાં આવે કે જેથી તે પાછો સપાટી પર આવે નહીં તેના માટે જરૂરી ન્યૂનતમ વેગ કેટલો હોવો જોઈએ? $($ ગ્રહ ની ત્રિજ્યા $6.4 \times {10^6}m,\,\,g = 9.8\,m/se{c^2})$View Solution
- 3$d$ અંતરે તેમજ $m$ અને $2\,m$ દળ ધરાવતાં બે તારાઓ મુક્ત અવકાશમાં તેમનાં સામાન્ય દ્રવ્યમાન કેન્દ્ર ને સાપેક્ષ પરિભ્રમણ કરે છે. પરિભ્રમણનો આવર્તકાળ ......... છે.View Solution
- 4View Solutionગુરુત્વાકર્ષી બળ માટે સામાન્ય રીતે ઉપવલયાકાર કક્ષા માટે શું સાચું છે ?
- 5બે ઉપગ્રહો $A$ અને $B$ ગ્રહને ફરતે અનુક્રમે $4R$ અને $R$ ત્રિજ્યાની વર્તુળાકર કક્ષામા ફરે છે. જે ઉપગ્રહ $A$ ની ઝડ૫ $3v$ હોય, તો $B$ ની ઝડપ. . . . . . થશે.View Solution
- 6$m$ અને $9m$ દળના બે પદાર્થને $R$ અંતરે મૂકેલા છે. આ બંને પદાર્થોને જોડતી રેખા પર જ્યાં ગુરુત્વાકર્ષણ ક્ષેત્ર શૂન્ય થાય તે બિંદુએ તેનું ગુરુત્વીય સ્થિતિમાન $.........$ હશે. ( $G=$ ગુરુત્વીય અચળાંક)View Solution
- 7એક પોલો ગોળો જેની ત્રિજ્યા $R$ છે તેના માટે ગુરુત્વસ્થિતિમાન વિરુદ્ધ અંતરનો ગ્રાફ નીચેના પૈકી કેવો દેખાય ?View Solution
- 8પૃથ્વીને $M$ દળનો અને $R$ ત્રિજયાનો એક ઘન ગોળો ધારો. જો પૃથ્વીની સપાટીથી નીચે $d$ ઉંડાઇએ ગુરુત્વપ્રવેગનું મૂલ્ય પૃથ્વીની સપાટીથી $h$ ઊંચાઈ ઉપરના ગુરુત્વપ્રવેગ જેટલું અને જે $\frac{g}{4}$ છે, (જયાં $g$ એ પૃથ્વીની સપાટી પરના ગુરુત્વપ્રવેગનું મૂલ્ય છે.) તો $\frac{h}{d}$ નો ગુણોત્તર થશે.View Solution
- 9View Solutionજો એક ગ્રહ પરનો ગુરુત્વપ્રવેગ પૃથ્વીના ગુરુત્વપ્રવેગ કરતાં બમણો અને ત્રિજ્યા પૃથ્વીની ત્રિજ્યા કરતાં બમણી હોય તો તે ગ્રહ પર પદાર્થની નિષ્ક્રમણ ઝડપ કેટલી થાય?
- 10પૃથ્વીને સંપૂર્ણ ગોળ માનીએ તો સપાટી થી $100 \,km$ ઊંડાઇએ ગુરુત્વ પ્રવેગ ........ $m/{s^2}$ થાય. ($R =6400\, km$ )View Solution
