ક્લોરિનની ઇલેક્ટ્રોન બંધુતા $3.7\,eV$ છે. $1$ ગ્રામ ક્લોરિનનું વાયુ અવસ્થામાં સંપૂર્ણપણે $Cl^-$ માં રૂપાંતર કરવામાં આવે છે .$(1\,eV = 23 .06\,kcal\,mol^{-1})$. આ પ્રક્રમમાં મુક્ત થતી ઉર્જા ......$kcal$ .
AIEEE 2012, Medium
Download our app for free and get started
d
Number of moles \(= \frac {1}{35.5}\)
Number of moles \(= \frac {1}{35.5}\)
Given, \(1\,eV = 23.06\,kcal\,mol^{-1}\)
\(3.7\,eV = 3.7 \times 23.06\,kcal\,mol^{-1}\)
i.e. \(1\) mole realease enegry
\(=3.7 \times 23.06\,kcal\)
\(\therefore \) Energy released
\(=\frac{1}{35.5}\times 3.7\times 23.06\,kcal=2.4\,kcal\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$25^{\circ} C$ અને $1$ વાતા દબાણે દહન એન્થાલ્પીનો નીયે આપેલ છે.View Solution
પદાર્થ $H _{2}$ $C$(ગ્રેફાઈટ) $C _{2} H _{6}( g )$ $\frac{\Delta_{ C } H ^{\Theta}}{ kJmol ^{-1}}$ $-286.0$ $-394.0$ $-1560.0$ તો,ઈથેનની સર્જન એન્થાલ્પી ........
- 2આપેલ આક્રૂતિને ધ્યાનમાં લો.View Solution
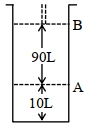
$18^{\circ} \mathrm{C}$ પર, સ્થાન $A$ પર, પિસ્ટન સાથે જોડેલા (fitted) સિલિન્ડર માં આદર્શ વાયુનો $1$ $\mathrm{mol}$ રાખેલ છે. જો તાપમાન માં કોઈપણ જાતનો ફેરફાર ન કરીએ તો પિસ્ટન એ સ્થાન $B$ તરફ ખસે છે ત્યારે આ પ્રતિવર્તી પ્રક્રમ માં થયેલ કાર્ય $'x' L atm$ છે. $x=-$ ........... $L.atm$ (નજીક નો પૂર્ણાક)
[આપેલ : નિરપેક્ષ તાપમાન $={ }^{\circ} \mathrm{C}+273.15, \mathrm{R}=0.08206 \mathrm{~L} \mathrm{~atm} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$ ]
- 3સમાન તાપમાને $CH_4, C_2H_6, C_2H_4$ અને $C_2H_2$ વાયુઓની દહન ઉષ્મા અનુક્રમે $-212.8, -373.0, -337.0$ અને $-310.5\, Kcal$ છે. તો આ વાયુઓ પણ શ્રેષ્ઠ બળતણ કયું છે?View Solution
- 4$350\,K$ પર આદર્શ વાયુ અને $4\,atm$ થર્મલ વાહક દિવાલોના $2.0\,L$ પાત્રમાં હોય છે, જે પર્યાવરણના સંપર્કમાં હોય છે.તે $4\,atm$ ના અચળ દબાણ વિરુદ્ધ સમતાપી પ્રતિવર્તી $........\,J\,K ^{-1}$ છે.(નજીકનો પૂર્ણાક) આપેલ : $R =8.314\,J\,K ^{-1}\,mol ^{-1}$.View Solution
- 5$300\, K$ તાપમાને પર એક આદર્શ વાયુનો એક મોલ $1$ લિટરના પ્રારંભિક કદથી $10$ લિટર સુધીનો સમતાપી રીતે વિસ્તૃત થાય છે. આ પ્રક્રિયા માટે $\Delta E$નું મૂલ્ય છે $(R = 2\, cal\, mol^{-1}\, K^{-1})$View Solution
- 6View Solutionરાસાયણિક પ્રક્રિચાઓના નીચેની ક્યા જોડકા ચોક્કસપણે પ્રક્રિયાની સ્વયંભૂયિતા દર્શાવશે ?
- 7$2C_8H_{18}$$_{(g)}$ $+$ $25$$O_2$$_{(g)}$ $\rightarrow$ $16$$CO_2$$_{(g)}$ $+ 18$ $H_2O$$_{(g)}$ પ્રક્રિયા વાહનોમાં થાય છે. $\Delta H$, $\Delta S$ અને $\Delta G$ ની સંજ્ઞા શું થશે ?View Solution
- 8$0\,^oC$ એ $1 \,kg$ બરફનું ગલન દરમિયાન થતો એન્ટ્રોપી ફેરફાર $SI$ એકમમાં ગણો. બરફની ગલન ઉષ્મા = $80\, cal \,g^{-1}$ ....$JK^{-1} \,gm^{-1}$View Solution
- 9$Cl_2$$_{(g)}$ $\rightarrow$ $2Cl$$_{(g)}$, આ પ્રક્રિયામાં $\Delta$ $H$ નું મૂલ્ય .......View Solution
- 10નીચે આપેલ માહિતી પરથી $OH^-$ આયનની સર્જન-ઉષ્માની કીમત $252\,^oC$ તાપમાને.....$KJ$ શોધો.View Solution
${H_2}{O_{(l)}} \to \,\,H_{(aq)}^ + + \,\,OH_{(aq)}^ - \,;\,\,\,\Delta H\,\, = \,\,57.32\,\,KJ\,;$
${H_2}_{(g)} + \,\,\frac{1}{2}\,\,{O_2}_{(g)} \to \,\,{H_2}{O_{(1)}}\,;\,\,\Delta H\,\, = \,\, - 286.20\,\,KJ$