કોઈ ચોક્કસ સ્થાને (સ્ટેશને) ટીવી ટ્રાન્સમીશન ટાવરની ઊંચાઈ $100 \,m$ છે. તેની કવરેજ અવધિ ત્રણ ગણી કરવી હોય તો ટાવરની ઊંચાઈ ..........$m$ સુધી વધારવી પડશે.
JEE MAIN 2022, Medium
d
Let \(d\) be range
Let \(d\) be range
\(d ^{2}=( h + R )^{2}- R ^{2}\)
\(= h ^{2}+ R ^{2}+2 RH - R ^{2}\)
\(d ^{2}= h ^{2}+2 Rh\)
\(\text { as } R \gg \gg \text { h then }\)
\(d \approx \sqrt{2 Rh } . \ldots . \text { (1) }\)
Now, if coverage is to be increased \(3\) times
\(3 d =\sqrt{2 Rh ^{\prime}} \ldots \text {. (2) }\)
Divide \(2\) and \(1 \frac{3 d }{ d }=\sqrt{\frac{2 R h^{\prime}}{2 R h}}\)
\(9=\frac{ h ^{\prime}}{ h }\)
\(9\,h = h \text { ' }\)
\(\text { If } h =100 m \text { then tower of height } 900 m \text { is } \text { required }\)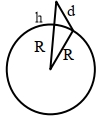
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઓપ્ટીકલ ફાબઇર માટે કોર અને કલેડીંગના વક્રીભવનાંક $\mu _1 $અને $\mu _2$ છે,પ્રકાશનું લીકેજ અટકાવવા માટે....View Solution
- 2$Twisted\,\, pair\,\, wire$ ની મદદથી કયા ગાળાની આવૃતિના સિગ્નલો પ્રસારિત કરી શકાય ?View Solution
- 3એક $TV$ ટ્રાન્સમિટરના એન્ટેનાની ઉંચાઈ $100 m$ છે. આ ટ્રાન્સમિટર કેટલા ક્ષેત્રફળ ધરાવતાં કાર્યક્રમોનું પ્રસારણ કરી શકશે ? $ (R = 6.4 \times 10^{6} m)$View Solution
- 4કંપવિસ્તાર અધિમિશ્રણ (એમ્પ્લિટ્યુડ મોડ્યલેશન) કરવાના પ્રયોગમાં, કિસ્સા $I$ માં,$X$ તેટલો કંપવિસ્તાર ધરાવતા બેઝ બેન્ડ સિગ્નલને $Y$ વોલ્ટ કંપવિસ્તાર ધરાવતા કેરિયર સિગ્નલ ઉપરાંત સંપાત કેરિયર કરવામાં આવે છે. ત્યારબાદ, કિસ્સા$-II$ માં, આ સમાન બેઝ બેન્ડ સિગ્નલને જુદા $2Y$ વોલ્ટ કંપવિસ્તાર ધરાવતાં કેરિયર સિગ્નલ ઉપર સંપાત કરવામાં આવે છે, આ બંને કિસ્સામાં અનુક્રમે અધિમિશ્રણ અંકનો ગુણોતર $..........$ થશે.View Solution
- 5$AM$ તરંગમાં રહેલ કુલ પાવર $900 W$ છે $100%$ મોડ્યુલેશન માટે બેન્ડદીપ ટ્રાન્સમીટ થતો પાવર...$ W$View Solution
- 6આધુનિક ઓપ્ટિકલ ફાઈબર સંચારમાં વપરાતા કેરિયર તરંગની તરંગલંબાઈ ......$nm$ નજીકની હોય છે?View Solution
- 7$250 pF$ ની કૅપેસિટી ધરાવતા કૅપેસિટર અને સમાંતરમાં $100 k\Omega$ નો અવરોધ ધરાવતા ડાયોડ ડિરેક્ટરનો ઉપયોગ $60%$ મૉડ્યુલેશન ધરાવતા ઍમ્પ્લિટ્યુડ મૉડ્યુલેટેડ તરંગને ડિરેક્ટ કરવામાં થાય છે. આ પરિપથથી ડિરેક્ટ થતી મહત્તમ મૉડ્યુલેશન આવૃત્તિ કેટલી હશે ?View Solution
- 8View Solutionમાઇક્રોવેવ ઓવન ક્યાં સિધ્ધાંત પર કાર્ય કરે છે?
- 9View Solutionઉપગ્રહીય સંદેશા વ્યવહાર માટે, ઉપયોગમાં લેવામાં આવતો ઉપર જોડાણ આવૃત્તિ પટ્ટ છે
- 10$1kHz$ આવૃત્તિવાળા તરંગનું ક્ષમતાપૂર્વક વિકિરણ કરવા માટે ઍન્ટેનાની લંબાઈ ઓછામાં ઓછી કેટલા ........$km$ રાખવી જોઈએ ?View Solution
