(d) \(x = a\cos (pt)\) and \(y = b\sin (pt)\) (given)
\(\therefore \) \(\cos pt = \frac{x}{a}\) and \(\sin pt = \frac{y}{b}\)
By squaring and adding
\({\cos ^2}(pt) + {\sin ^2}(pt) = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Hence path of the particle is ellipse.
Now differentiating \(x\) and \(y\) w.r.t. time
\({v_x} = \frac{{dx}}{{dt}} = \frac{d}{{dt}}(a\cos (pt)) = - ap\sin (pt)\)
\({v_y} = \frac{{dy}}{{dt}} = \frac{d}{{dt}}(b\sin (pt)) = bp\cos (pt)\)
\(\therefore \;\;\vec v = {v_x}\hat i + {v_y}\hat j = - ap\sin (pt)\hat i + bp\cos (pt)\hat j\)
Acceleration \(\vec a = \frac{{d\vec v}}{{dt}} = \frac{d}{{dt}}[ - ap\sin (pt)\hat i + bp\cos (pt)\hat j]\)
\(\vec a = - a{p^2}\cos (pt)\;\hat i - b{p^2}\sin (pt)\hat j\)
Velocity at \(t = \frac{\pi }{{2p}}\)
\(\vec v = - ap\sin p\left( {\frac{\pi }{{2p}}} \right)\;\hat i + bp\cos p\left( {\frac{\pi }{{2p}}} \right)\hat j\)\( = - ap\;\hat i\)
Acceleration at \(t = \frac{\pi }{{2p}}\)
\(\vec a = a{p^2}\cos p\left( {\frac{\pi }{{2p}}} \right)\;\hat i - b{p^2}\sin p\left( {\frac{\pi }{{2p}}} \right)\hat j\)\( = - b{p^2}\hat j\)
As \(\vec v\;.\;\vec a = 0\)
Hence velocity and acceleration are perpendicular to each other at \(t = \frac{\pi }{{2p}}\).
Download our appand get started for free
Similar Questions
- 1$R ^{3}$ નાં વ્યસ્ત પ્રમાણમાં ચલિત કેન્દ્રીય આભાસી બળ $F$ ની અસર હેઠળ એક કણ અચળ ઝડપથી $R$ ત્રિજ્યા ધરાવતાં વર્તુળનાં પરીઘ પર ગતિ કરે છે. તેનાં પરિભ્રમણનો આવર્તકાળ ......... દ્વારા દર્શાવવામાં આવે છે.View Solution
- 2View Solutionનિયમિત કોણીય ગતિ દરમિયાન નીચે આપેલ કઈ રાશિ અચળ રહે છે?
- 3View Solutionઘડિયાળમાં મિનિટ કાંટો અને કલાક કાંટાનો કોણીય ઝડપનો ગુણોત્તર કેટલો થાય?
- 4પ્રાક્ષિપ્ત પદાર્થનું સમીકરણ $y=a x-b x^2$ છે. તેની સમક્ષિતીજ અવધી શું હશે?View Solution
- 5એક કણ ઉગમબિંદુથી $x-y$ સમતલમાં પોતાની ગતિ શરૂ કરે છે. $\mathrm{t}=0$ સમયે તેનો શરૂઆતનો વેગ $3.0 \hat{\mathrm{i}} \;\mathrm{m} / \mathrm{s}$ અને અચળ પ્રવેગ $(6.0 \hat{\mathrm{i}}+4.0 \hat{\mathrm{j}}) \;\mathrm{m} / \mathrm{s}^{2}$ છે. જ્યારે કણનો $y-$યામ $32\;\mathrm{m}$ હોય ત્યારે તેનો $x-$યામ $D$ મીટર છે તો $D$ નું મૂલ્ય કેટલું હશે?View Solution
- 6એક વિમાન $490 \,m$. ઊંચાઇ પર $60 \,km/hr$ ના સમક્ષિતિજ વેગથી ઉડી રહ્યું છે. $A$ બિંદુની બરાબર ઉપર વિમાન હોય ત્યારે,તેમાંથી પદાર્થને પડતો મૂકતા તે $A$ બિંદુથી કેટલા અંતરે પડશે? $(g = 9.8 m/s^2)$View Solution
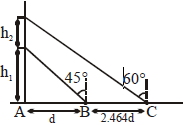
- 7એક બલૂન જમીન પર રહેલ બિંદુ $A$ થી ઉપર તરફ શિરોલંબ દિશામાં ગતિ કરે છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે જ્યારે એક છોકરી (જે બિંદુ $B$ પર છે ) જે $A$ બિંદુથી $d$ અંતરે છે, તે બલૂન જ્યારે $h_1$ ઊંચાઈ પર પહોચે ત્યારે તે બલૂનને શિરોલંબ સાથે $45^{\circ}$ ના ખૂણે જોવે છે. જ્યારે બલૂન જ્યારે $h_2$ ઊંચાઈ પર પહોચે ત્યારે તે $2.464\, d$ જેટલું અંતર ખસીને(બિંદુ $C$ પર) બલૂનને શિરોલંબ સાથે $60^{\circ}$ ના ખૂણે જોવે છે. તો ઊંચાઈ $h _{2}$ કેટલી હશે? ($\tan \left.30^{\circ}=0.5774\right)$View Solution
- 8$7 \,km / hr$ ની ઝડપે ઉત્તર તરફ જતાં એક મોટરકારના ચાલકને બસ $25 \,km / hr$ ની ઝડપે જતી લાગે છે. જો બસ ખરેખર પૂર્વ દિશામાં ગતિ કરતી હોય તો તેની ઝડપ ............. $km / h$ હશે?View Solution
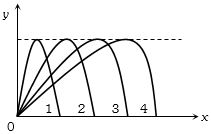
- 9View Solutionનીચેની આકૃતિમાં વેગના સમક્ષિતિજ ઘટકના મૂલ્ય ઉત્તરતા ક્રમમાં
- 10$20m$ વળાંકવાળો બ્રિજને કાર સંપર્ક છોડયા વગર પસાર કરવા માટે કારની ઝડપ કેટલા........$m/s$ રાખવી જોઇએ? $(g = 9.8\;m/{s^2})$View Solution
