Here, \(V(x, y, z)=6 x-8 x y-8 y+6 y z\)
The \(x, y\) and \(z\) components of electric field are
\(E_{x} =-\frac{\partial V}{\partial x}=-\frac{\partial}{\partial x}(6 x-8 x y-8 y+6 y z)\)
\(=-(6-8 y)=-6+8 y\)
\(E_{y} =-\frac{\partial V}{\partial y}=-\frac{\partial}{\partial y}(6 x-8 x y-8 y+6 y z)\)
\(=-(-8 x-8+6 z)=8 x+8-6 z\)
\(E_{z} =-\frac{\partial V}{\partial z}=-\frac{\partial}{\partial z}(6 x-8 x y-8 y+6 y z)=-6 y \)
\(\vec{E} =E_{x} \hat{i}+E_{y} \hat{j}+E_{z} \hat{k}\)
\(=(-6+8 y) \hat{i}+(8 x+8-6 z) \hat{j}-6 y \hat{k}\)
At point \((1,1,1)\)
\(\bar{E}=(-6+8) \hat{i}+(8+8-6) \hat{j}-6 \hat{k}=2 \hat{i}+10 \hat{j}-6 \hat{k}\)
The magnitude of electric field \(\vec{E}\) is
\(\vec{E}=\sqrt{E_{x}^{2}+E_{y}^{2}+E_{z}^{2}}=\sqrt{(2)^{2}+(10)^{2}+(-6)^{2}}\)
\(=\sqrt{140}=2 \sqrt{35} \,{N} {C}^{-1}\)
Electric force experienced by the charge \(F=q E=2 \mathrm{C} \times 2 \sqrt{35} \mathrm{\,NC}^{-1}=4 \sqrt{35}\mathrm{\,N}\)
Download our appand get started for free
Similar Questions
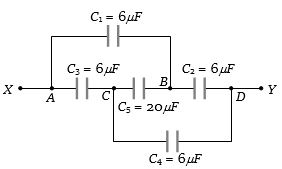
- 1આપેલ પરિપથમાં $X$ અને $Y$ વચ્ચે સમતુલ્ય કેપેસિટન્સ કેટલા.........$\mu F$ થાય?View Solution
- 2$R $ ત્રિજયાવાળા વાહક પોલા ગોળાની સપાટી પર $Q$ વિધુતભાર આપવામાં આવે છે. તેના કેન્દ્ર પર વિધુતસ્થિતિમાન અને વિદ્યુતક્ષેત્ર અનુક્રમે કેટલા મળે?View Solution
- 3સમાંતર પ્લેટ કેપેસીટરની પ્લેટ વચ્ચેનું અંતર $d$ , પ્લેટનું ક્ષેત્રફળ $A$ અને $K$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતા દ્રવ્ય કેપેસીટરનું કેપેસીટન્સ $C_0$ છે. તેમાંથી ત્રીજા ભાગનું દ્રવ્ય $2K$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતા દ્રવ્ય વડે બદલવામાં આવે છે, કે જેથી તેમાં પરિણામી બે કેપેસીટર એક $\frac{1}{3}\,A$ ક્ષેત્રફળવાળો ,જેનો ડાઈઇલેક્ટ્રિક અચળાંક $2K$ અને બીજો $\frac{2}{3}\,A$ ક્ષેત્રફળવાળો ,જેનો ડાઈઇલેક્ટ્રિક અચળાંક $K$ થાય.જો નવા કેપેસીટરનો કેપેસીટન્સ $C$ હોય તો $\frac{C}{{{C_0}}}$ નો ગુણોત્તર કેટલો થાય?View Solution
- 4$a$ અને $b$ (જ્યાં $a < b)$ ત્રિજ્યાઓ ધરાવતા ગોળાઓ $A$ અને $B$ એકબીજાથી ખૂબ જ લાંબા અંતરે છે.બંને ગોળાઓ પર $100\,\mu C$ જેટલો ચાર્જ રહેલ છે, જો બંને ગોળાઓને વાહક તાર વડે જોડવામાં આવે તો નીચેનામાંથી ક્યું પરીણામ મળે?View Solution
- 5એક કણ $A$ અનો વિદ્યુતભાર $+q$ અને $B$ નો વિદ્યુતભાર $+9\ q$ છે. પ્રત્યેક કણનું દળ $m$ સમાન છે. જો બંને કણોને સ્થિર સ્થિતિએથી સમાન સ્થિતિમાન તફાવત સાથે છોડવામાં આવે તો તેઓની ઝડપનો ગુણોત્તર ....... હશે.View Solution
- 6વિધાન $-1$ : વાહક પદાર્થનો ઉપયોગ કરીને $1$ ફેરાડે ક્ષમતા ધરાવતો ગોળો બનાવી શકાય નહીંView Solution
વિધાન $-2$ : $6.4\times10^6\, m$ ત્રિજ્યા ધરાવતી પૃથ્વી માટે આ શક્ય છે.
- 7વિદ્યુતબળ રેખાઓ અને સમસ્થિતિમાન પૃષ્ઠ વચ્ચેનો કોણ $......$ હશે.View Solution
- 8$C$ જેટલો કેપેસીટન્સ ધરાવતા કેપેસીટરને $200\,V$ ની બેટરી વડે ચાર્જ કરવામાં આવે છે. જ્યારે આા કેપેસીટરને ઉષ્મીય રીતે ચુસ્ત કરેલ એવા બ્લોક વડે ડીસ્ચાર્જ કરેલ છે કે જેનો વિશિષ્ટ ઉષ્મા ક્ષમતા $2.5 \times 10^2 J / kg$ અને દળ $0.1\,kg$. છે. જો આા બ્લોકનું તાપમાન $0.4\,K$ જેટલું વધે તો $C$ નું મુલ્ય શોધો.View Solution
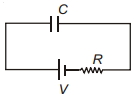
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે, $C$ ક્ષમતા ધરાવતા કેપેસીટર સાથે $R$ જેટલો અવરોધ જોંડલ છે. બેટરી દ્વારા આપવામાં આવતી ઊર્જા કેટલી હશે?View Solution
- 10$K$ ડાઈઇલેક્ટ્રિક ધરાવતા માધ્યમમાં વિદ્યુતક્ષેત્ર $\vec E$ છે. જો શૂન્યાવકાશની પરમિટિવિટી ${ \varepsilon _0}$ હોય તો વિદ્યુતસ્થાનાંતર સદીશ કેટલો થાય?View Solution
