$L$ લંબાઈ અને $M$ દળની લાકડી ઘર્ષણ રહિત સપાટી પર કોઇ પણ રીતે મુક્ત પણે ગતિ કરી શકે છે. $ m$ દળનો બોલ $ v$ ઝડપથી આકૃતિમાં દર્શાવ્યા પ્રમાણે ગતિ કરે છે. બોલનું દળ કેટલું હોવું જોઈએ કે જેથી અથડામણ બાદ તે સ્થિર રહે ?
Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2\ meter$ બાજુવાળા ચોરસના ખૂણા પર $m$ દળના કણો મૂકેલા છે.જો તેમના વિકર્ણના છેદનબિંદુને ઉગમબિંદુ લેવામાં આવે તો ચોરસના દ્રવ્યમાન કેન્દ્રના યામ શું થાય?View Solution
- 2$1\,kg$ દળ ધરાવતો એક નિયમિત ગોળો સમતલ સપાટી ઉપર સરક્યા સિવાય ગબડે છે. તેને $7 \times 10^{-3}\,J$ જેટલી ગતિઉર્જા છે. ગોળાના દ્રવ્યમાન કેન્દ્રની ઝડપ $...........\,cm s ^{-1}$ હશે.View Solution
- 3$V _{ CM }=2\; m / s , m =2\;kg , R =4 \;m$ જ્યારે રીંગ સંપૂર્ણ ગબડે ત્યારે તેનું કોણીય વેગમાન ઉદગમબિંદુને અનુલક્ષીને ($kgm ^{2} / s$ માં)View Solution
- 4ટોર્ક મેળવવા માટે ઇલેકટ્રીક મોટરની ધરીનેે સ્થિર સ્થિતિમાંથી ગતિની શરૂઆત કરવામાં આવે છે. તે $\alpha = 3t - t^2$, જેટલું કોણીય પ્રવેગ પ્રાપ્ત કરે છે. તેની ચાકગતિની શરૂઆત થયાના $2\ seconds $ બાદ $\alpha = 0. $ થાય, તો $6\ seconds$ પછી તેનો કોણીય વેગ ગણો.View Solution
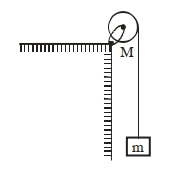
- 5$M=4 \,kg$ દળ અને $R=10 \,cm$ ત્રિજ્યા ધરાવતી એક નિયમિત તક્તિને સમક્ષિતિજ એક્સેલ (ધરી) સાથે આકૃતિમાં દર્શાવ્યા અનુસાર જડવામાં આવેલ છે. $m =2 \,kg$ દળ ધરાવતા ચોસલાને દળરહિત દોરી, કે જેને તક્તિના પરીઘ ઉપર વીંટાળેલ છે, ની મદદથી લટકાવવામાં આવેલ છે. ચોસલાના પતન દરમ્યાન દોરી (તક્તિ ઉપર) સરક્તી નથી અને ધરી માં ધર્ષણ નથી (તેમ ધારો). દોરીમાં તણાવ .............. $N$ હશે. ( $g =10 \,ms ^{-2}$ લો.)View Solution
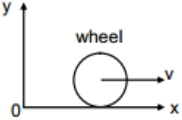
- 6પૃષ્ઠને લંબ એવા કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $I_1$ જડત્વની ચાકમાત્રા ધરાવતી તકતી આ અક્ષને અનુલક્ષીને $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. હવે, પૃષ્ઠને લંબ એવા કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $I_2$ જેટલી જડત્વની ચાકમાત્રા ધરાવતી બીજી તકતી આ તકતી પર મૂકવામાં આવે, તો આ બંને તકતીનો સંયુક્ત કોણીય વેગ કેટલો હશે ?View Solution
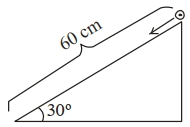
- 7$30^{\circ}$ ખૂણો અને $60\,cm$ લંબાઈવાળા ઢળતા સમતલની ટોચ પરથી એક નક્કર નળાકારને સ્થિર સ્થિતિમાંથી સિલિન્ડર મુક્ત કરવામાં આવે છે. જો નળાકાર સરક્યાં વગર ગબડે છે, તો ઢોળાવવાળા સમતલના તળિયે પહોંચતા તેની ઝડપ $(ms ^{-1}$ માં) કેટલી થાય? (આપેલ $g =10\,ms ^{-2}$)View Solution
- 8દરેક $M$ દળ ધરાવતા ત્રણ એક સમાન ગોળાઓને કાટકોણ ત્રિકોણના ખૂણાઓ (શિરોબિંદુ) પર મૂકવામાં આવ્યા છે. કાટકોણ ત્રિકોણની એકબીજાને લંબ બાજુ $3\,m$ ની છે. આ બે એકબીજાને લંબ બાજુનાં અંતઃ છેદને ઉગમ બિંદુ તરીકે લઈ દ્રવ્યમાન કેન્દ્રના સ્થાન સદિશના માનાંક $\sqrt{x} m$ છે, તો $x=........$ થશે.View Solution
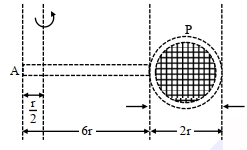
- 9આકૃતિમાં એક બેડમિન્ટન રેકેટના પરિમાણ આપેલા છે. જો બેડમિન્ટનના રેખીય અને વર્તુળાકાર ભાગનું સમાન દળ $(M)$ અને દોરીનું દળ અવગણ્ય હોય તો, હેન્ડલના બિંદુ $A$ થી $\frac{r}{2}$ અંતરે રેકેટના હેન્ડલને લંબ અને રિંગના સમતલમાં રહેલી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ....... $Mr^2$ જેટલી થાય?View Solution
- 10View Solutionઅચળ કોણીય ઝડપથી ગતિ કરતું પૈડુ ગતિ દરમિયાન બ્રેકનો અનુભવે કરે તો તેની ચક્રાવર્તનની ત્રિજ્યા =…..