$L$ મીટર બાજુવાળો ચોરસ પેપરના સમતલમાં છે. સમાન વિદ્યુતક્ષેત્ર $\vec E\;(V/m) $ પેપરના સમતલમાં છે, પણ તે ચોરસના નીચેના અડધા વિસ્તારમાં સીમિત છે. (આકૃતિ જુઓ) પૃષ્ઠ સાથે સંકળાયેલ વિદ્યુતફલક્સ $SI$ એકમમાં કેટલું હશે?
AIPMT 2006, Easy
Download our app for free and get started
d
\(\phi=\overrightarrow{ E } \cdot \overrightarrow{ S }= ES \cos 90^{\circ}=0\)
\(\phi=\overrightarrow{ E } \cdot \overrightarrow{ S }= ES \cos 90^{\circ}=0\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસમાંગ વિદ્યુતક્ષેત્રમાં મૂકેલ વિદ્યુત ડાયપોલ કઈ સ્થિતિમાં બળયુગ્મની મહત્તમ ચાકમાત્રા અનુભવે છે ?
- 2View Solutionવિદ્યુત બળ રેખાઓની દિશામાં તેના વેગ સાથે ઈલેકટ્રોન તેના વિદ્યુતક્ષેત્રમાં દાખલ થાય તો.......
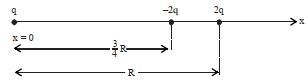
- 3ત્રણ બિંદુવત વીજભારો $q,-2 q$ અને $2 q , x$-અક્ષ પર $x=0, x=\frac{3}{4} R$ અને $x=R$ અંતરે અનુક્રમે ઉદગમથી મૂકેલા આકૃતિમાં દર્શાવેલ છે. જો $q =2 \times 10^{-6}\,C$ અને $R=2\,cm$ હોય તો $-2 q$ વિદ્યુતભારને અનુભવતું પરિણામી બળ ..........$N$ છે.View Solution
- 4$20$ યુનિટ ક્ષેત્રફળ ધરાવતી સપાટી $Y-Z$ સમતલમાં છે,જો વિદ્યુતક્ષેત્ર $(5 \hat{i}+4 \hat{j}+9 \hat{k})$ હોય તો સપાટીમાંથી પસાર થતું ફલક્સ શોધો. (એકમ માં)View Solution
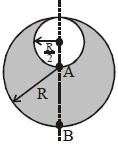
- 5$\mathrm{R}$ ત્રિજ્યા ધરાવતા ગોળા પર વિજભારઘનતા $\rho$ છે.જો તેમાથી $\frac{\mathrm{R}}{2}$ ત્રિજ્યા ધરાવતો ભાગ કાપી નાખવામાં આવે તો $\frac{\left|\overrightarrow{\mathrm{E}}_{\mathrm{A}}\right|}{\left|\overrightarrow{\mathrm{E}}_{\mathrm{B}}\right|}$ નો ગુણોત્તર કેટલો થાય? જ્યાં $\overrightarrow{\mathrm{E}}_{\mathrm{A}}$ અને $\overrightarrow{\mathrm{E}}_{\mathrm{B}}$ બિંદુ $\mathrm{A}$ અને બિંદુ $\mathrm{B}$ પાસે વિદ્યુતક્ષેત્ર છે.View Solution
- 6$0.1 \,\mu m$ ત્રિજ્યાનો એક વિદ્યુતભારતીત પાણીનું ટીપુ વિદ્યુતક્ષેત્રની સંતુલન અવસ્થા હેઠળ આવેલ છે. ટીપા પરનો વિદ્યુતભાર ઈલેકટ્રોનીક્સ વિદ્યુતભારને સમતુલ્ય છે. વિદ્યુતક્ષેત્રની તીવ્રતા ........$N/C$ છે.View Solution
- 7બે બિંદુવત વિદ્યુતભારો $q_2$ = $3 \times 10^{-6}\ C$ અને $q_1$ =$ 5 \times 10^{-6}\ C$ એ $B \,(3, 5, 1)\ m $ આગળ અને $A\, (1, 3, 2)\ m$ આવેલા છે. $q_2$ ના લીધે $q_1$ પર બળનું મૂલ્ય શોધો.View Solution
- 8$20$ યુનિટ ક્ષેત્રફળ ધરાવતી સપાટી $Y-Z$ સમતલમાં છે,જો વિદ્યુતક્ષેત્ર $(5 \hat{i}+4 \hat{j}+9 \hat{k})$ હોય તો સપાટીમાંથી પસાર થતું ફલક્સ શોધો. (એકમ માં)View Solution
- 9$p$ ડાયપોલ મોમેન્ટ ધરાવતા ડાયપોલનું કેન્દ્ર ઉદ્ગમબિંદુ પર રહે તે રીતે $x$-અક્ષ પર મૂકેલ છે.ડાયપોલના કેન્દ્રથી અમુક અંતરે આવેલા બિંદુને જોડતી રેખાએ $x$-અક્ષ સાથે બનાવેલો ખૂણો $\theta $ છે.તો તે બિંદુએ વિદ્યુતક્ષેત્રએ $x$-અક્ષ સાથે કેટલો ખૂણો બનાવે? [ $\tan \alpha = \frac{1}{2}\tan \theta $ ]View Solution
- 10View Solutionદ્વિ ધ્રુવીય ચાકમાત્રાનો એકમ ......... છે.