અદીશ \(\mathop {\rm{A}}\limits^ \to \,\, = \,\,2\hat i\,\, + \;\,3\hat j\,\, + \;\,\hat k\) અને અદીશ \(\mathop B\limits^ \to \,\, = \,\,\hat i\,\, - \,\,\hat j\,\, + \;\,2\hat k\)
\(\vec A \) અને \(\vec B \) નો લંબ એકમ સદીશ \(\hat n\, = \,\,\frac{{\mathop A\limits^ \to \,\, \times \,\,\mathop B\limits^ \to }}{{|\mathop A\limits^ \to \,\, \times \,\,\mathop B\limits^ \to |}}\)
\(\,\,\mathop A\limits^ \to \,\, \times \,\,\mathop B\limits^ \to \,\, = \,\,\left| {\left. {\begin{array}{*{20}{c}}
{\hat i}&{\hat j}&{\hat k}\\
2&3&1\\
1&{ - 1}&2
\end{array}} \right|} \right.\,\, = \,\,\hat i\left( {6\,\, + \;\,1} \right)\,\, - \,\,\hat j\,\,\left( {4\,\, - \,\,1} \right)\,\, + \;\,\hat k\,\,\left( { - 2\,\, - \,\,3} \right)\,\, = \,\,7\hat i\,\, - \,\,3\hat j\,\, - \,\,5\hat k\)
\(\,|\mathop A\limits^ \to \,\, \times \,\,\mathop B\limits^ \to |\,\, = \,\,\sqrt {{7^2}\,\, + \;\,{{\left( { - 3} \right)}^2}\,\, + \;\,{{\left( { - 5} \right)}^2}} \,\, = \,\,\sqrt {83} \) એકમ
\(\therefore \,\hat n\,\, = \,\,\frac{1}{{\sqrt {83} }}\,\,\left( {7\hat i\,\, - \,\,3\hat j\,\, - \,\,5k} \right)\)
Download our appand get started for free
Similar Questions
- 1જો $\overrightarrow A \times \overrightarrow B=\overrightarrow B \times \overrightarrow A$ , તો $ \overrightarrow A $ અને $ \overrightarrow B $ વચ્ચેનો ખૂણો કેટલો હશે?View Solution
- 2સ્થિર અવસ્થામાં રહેલો પદાર્થ પર ત્રણ બળ સદીશ $2 \hat{i}+2 \hat{j}, 2 \hat{i}-2 \hat{j}$ અને $-4 \hat{i}$ દ્વારા લગાવવામાં આવે છે. તો પદાર્થ કઈ દિશામાં ગતિ કરશે?View Solution
- 3નીચેનામાંથી કઈ રાશિ/ રાશિઓ યામોક્ષોનાં અભિગમની પસંદગી પર આધાર રાખે છે?View Solution
$(a)$ $\vec{a}+\vec{b}$
$(b)$ $3 a_x+2 b_y$
$(c)$ $(\vec{a}+\vec{b}-\vec{c})$
- 4કાર્તેઝિયન યામ પદ્ધતિમાં સદિશોView Solution
$ \vec a = 4\hat i - \hat j $ , $ \vec b = - 3\hat i + 2\hat j $ અને $ \vec c = - \hat k $ છે.
જ્યાં $\hat i,\,\hat j,\,\hat k$ એ અનુક્રમે $X,Y,Z$ ની દિશામાનો એકમ સદીશ છે તો તેના પરિણામી સદિશની દિશામાંનો એકમ સદિશ $\hat r$ શું મળે ?
- 5જો $\overrightarrow{ P } \times \overrightarrow{ Q }=\overrightarrow{ Q } \times \overrightarrow{ P }$ હોય તો $\overrightarrow{ P }$ અને $\overrightarrow{ Q }$ વચ્ચેનો કોણ $\theta\left(0^{\circ} < \theta < 360^{\circ}\right)$ છે. જ્યાં $\theta$ નું મૂલ્ય ....... ડિગ્રી હશે.View Solution
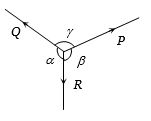
- 6$P, Q$ અને $R$ સદિશો એક બિંદુ પર લાગે છે,તે બિંદુ સમતોલનમાં હોય તો નીચેનામાથી કયું વિધાન સાચું છે?View Solution
- 7જો $\overrightarrow A \times \overrightarrow B=\overrightarrow B \times \overrightarrow A$ , તો $ \overrightarrow A $ અને $ \overrightarrow B $ વચ્ચેનો ખૂણો કેટલો હશે?View Solution
- 8જો સદિશ $ \overrightarrow A = 2\hat i + 4\hat j - 5\hat k $ ,હોય તો સદીશનો દિશાકીય cosine કેટલો થાય?View Solution
- 9$A$ અને $\frac{A}{2}$ નાં મૂલ્યો ધરાવતા બે બળો એકબીજાને લંબ છે. તેનું પરિણામીનું મૂલ્ય ...... છે.View Solution
- 10જો સદિશ $2\hat i + 3\hat j - \hat k$ એ સદિશ $ - 4\hat i - 6\hat j + \lambda \hat k$ ને લંબ છે.તો $\lambda$ મેળવો.View Solution
