પ્રારંભિક વેગમાન \(= mv\) અથડામણ પછી જ્યારે સ્પ્રિંગ મહત્તમ સંકોચાય ત્યારે બ્લોક \(A\) અને \(B\) વેગ \(v\) સાથે ગતી કરે છે.
રેખીય વેગમાન સંરક્ષણના નિયમ મુજબ \(m\upsilon \,\, = \,\,(m\, + \,m)\,V\,\, \Rightarrow \,\,V\,\, = \,\,\frac{\upsilon }{2}\)
ઊર્જા સંરક્ષણના નિયમ મુજબ બ્લોક બે ગતિ ઊર્જા \(= A,B\) સિસ્ટમ ગતી ઉર્જા સ્થીરે ઊર્જા
\(\frac{1}{2}m{\upsilon ^2}\, = \,\,\frac{1}{2}(2m){V^2}\,\, + \,\,\frac{1}{2}\,k{x^2}\,\,\,\,\, \Rightarrow \,\,\frac{1}{2}m{\upsilon ^2}\,\, = \,\,\frac{1}{2}(2m)\,{\left( {\frac{\upsilon }{2}} \right)^2}\,\, + \,\,\frac{1}{2}k{x^2}\,\, \Rightarrow \,k{x^2}\,\, = \,\,\frac{1}{2}\,m{\upsilon ^2}\)
\(\, \Rightarrow \,x\,\, = \,\,\upsilon \,\,\sqrt {\frac{m}{{2k}}} \)
Download our appand get started for free
Similar Questions
- 1$200\,g$ નો એક બોલ $20\,m$ ઊંચા થાંભલા ઉપર સ્થિર સ્થિતિમાં છે.$10\,g$ ની અને $u\,m/s$ ના વેગથી સમક્ષિતિજ દિશામાં ગતિ કરતી એક ગોળી (બુલેટ) બોલના કેન્દ્રને અથડાય છે સંઘાત બાદ બંને એકબીજાથી સ્વતંત્ર રીતે ગતિ કરે છે.બોલ જમીન ઉપર થાંભલાના તળિયે થી $30\,m$ અંતરે અને બુલેટ $120\,m$ અંતરે પડે છે. બુલેટનો વેગ $..............m/s$ હશે.($\left.g =10 m / s ^2\right.$ છે.)View Solution
- 2$5 \times {10^3}N/m$ બળ અચળાંક ધરાવતી સ્પિંગ્રની લંબાઇ $ 5 cm$ થી $10 cm$ વધારતાં થતું કાર્ય......$N-m$View Solution
- 3$M=500\,kg$ દળ ધરાવતી એક લિફટ $(elevator\,cab)$ $2\,ms ^{-1}$ ની ઝડપથી નીચે ઉતરે છે. તેના આધાર માટેનો કેબલ સરકવાનું શરૂ કરે છે તેથી તે $2\,ms ^{-2}$ ના અચળ પ્રવેગથી પડવાનું શરૂ કરે છે. $6\,m$ ના અંતર સુધી પડયા બાદ લિફટની ગતિઊર્જા $..........kJ$ થશે.View Solution
- 4એક પ્રક્ષિપ્ત પદાર્થની તેની મહત્તમ ઉંચાઈએ સ્થિતિ - ઊર્જા તેની શરૂઆતની ગતિઊર્જાની $3/4 $ ગણી થાય છે, તો પદાર્થનો પ્રક્ષિપ્તકોણ ...... $^o$ છે.View Solution
- 5દ્વિ-પરમાણ્વીય અણુ માટે સ્થિતિ ઊર્જ $(U)$ આંતર આણ્વીય અંતર $r$ નું વિધેય છે, કે જેView Solution
$U =\frac{\alpha}{ r ^{10}}-\frac{\beta}{ r ^{5}}-3$
જ્યાં,$\alpha$ અને $\beta$ ધન અચળાંકો છે. બે પરમાણુઓ વચ્ચેનું સંતુલન અંતર $\left(\frac{2 \alpha}{\beta}\right)^{\frac{a}{b}}$ હશે જ્યાં $a=..........$ છે
- 6$ {m_A} $ અને $ {m_B} $ દળના વેગ $ {v_A} $ અને $ {v_B} $ છે.અથડામણ પછી $ {m_A} $ અને $ {m_B} $ દળના વેગ $ {v_B} $ અને $ {v_A} $ હોય,તો $ \frac{m_A}{m_B} =$ _____View Solution
- 7એક સાદું લોલક લાકડાનાં $50 \,g$ દળ ધરાવતા દોલક અને $2 \,m$ લંબાઈનું બનેલું છે. $75 \,g$ દળ ધરાવતી બુલેટ (ગોળી) ને $v$ જેટલા વેગથી લોલક તરફ ફાયર કરવામાં આવે છે. ગોળી દોલકમાંથી $\frac{v}{3}$ જેટલી ઝડપ સાથે બહાર આવે છે અને દોલક એક ઉર્ધ્વ (શિરોલંબ) વર્તુળ પૂર્ણ કરે છે. તો $v$ નું મૂલ્ય ............ $ms ^{-1}$ થશે. ( $g =10 \,m / s ^{2}$ લો.)View Solution
- 8પ્રારંભમાં સ્થિર પદાર્થ $2M $ અને $3M $ દળ ના બે ટૂકડામાં વહેંચાય છે અને તેમની બંનેની મળીને કુલ ગતિઊર્જા $E$ છે. ટૂકડામાં વહેંચાયા બાદ $ 2M$ દળના ટૂકડાની ગતિઊર્જા કેટલી હશે?View Solution
- 9$m$ દળનો પદાર્થ $v$ વેગથી ગતિ કરીને $m$ દળના પદાર્થ સાથે અસ્થિતિસ્થાપક સંધાત કરે છે.પહેલા પદાર્થનો વેગ $ \frac{v}{{\sqrt 3 }} $ થઇ જતો હોય,બીજા પદાર્થનો વેગ કેટલો થશે?View Solution
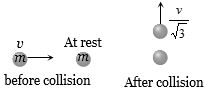
- 10બે સમાન દળ $m$ ધરાવતા બ્લોક $A$ અને $B$ સમક્ષિતિજ સપાટી પર $L$ લંબાઈ અને $K$ બળઅચળાંક ધરાવતી સ્પ્રિંગથી જોડેલા છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ત્રીજો $m$ દળનો બ્લોક $C$ એ $v$ વેગથી $A$ ને અથડાય છે. તો સ્પ્રિંગનું મહતમ સંકોચન કેટલું થાય?View Solution

