$m$ દળનો પદાર્થ $v$ વેગથી ગતિ કરીને $m$ દળના પદાર્થ સાથે અસ્થિતિસ્થાપક સંધાત કરે છે.પહેલા પદાર્થનો વેગ $ \frac{v}{{\sqrt 3 }} $ થઇ જતો હોય,બીજા પદાર્થનો વેગ કેટલો થશે?
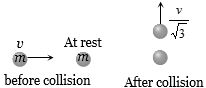
AIEEE 2005, Diffcult
a
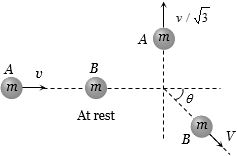
(a)Let mass \(A\) moves with velocity \(v\) and collides inelastically with mass \(B\), which is
According to problem mass \(A \) moves in a perpendicular direction and let the mass \(B \) moves at angle \(\theta\) with the horizontal with velocity \( v\).
Initial horizontal momentum of system
(before collision) \(= mv\) \(....(i)\)
Final horizontal momentum of system
(after collision) \(= mV\, cos\) \(\theta\)\( ....(ii)\)
From the conservation of horizontal linear momentum \(mv = mV \) \(cos\)\(\theta\)\(⇒\) \( v = V cos\)\(\theta\) \(...(iii)\)
Initial vertical momentum of system (before collision) is zero.
Final vertical momentum of system \(\frac{{mv}}{{\sqrt 3 }} - mV\sin \theta \)
From the conservation of vertical linear momentum \(\frac{{mv}}{{\sqrt 3 }} - mV\sin \theta = 0\)==>\(\frac{v}{{\sqrt 3 }} = V\sin \theta \)\(...(iv)\)
By solving \((iii)\) and \((iv)\)
\({v^2} + \frac{{{v^2}}}{3} = {V^2}({\sin ^2}\theta + {\cos ^2}\theta )\)
\(⇒\) \(\frac{{4{v^2}}}{3} = {V^2}\) \(⇒\)\(V = \frac{2}{{\sqrt 3 }}v\).
(a)Let mass \(A\) moves with velocity \(v\) and collides inelastically with mass \(B\), which is
According to problem mass \(A \) moves in a perpendicular direction and let the mass \(B \) moves at angle \(\theta\) with the horizontal with velocity \( v\).
Initial horizontal momentum of system
(before collision) \(= mv\) \(....(i)\)
Final horizontal momentum of system
(after collision) \(= mV\, cos\) \(\theta\)\( ....(ii)\)
From the conservation of horizontal linear momentum \(mv = mV \) \(cos\)\(\theta\)\(⇒\) \( v = V cos\)\(\theta\) \(...(iii)\)
Initial vertical momentum of system (before collision) is zero.
Final vertical momentum of system \(\frac{{mv}}{{\sqrt 3 }} - mV\sin \theta \)
From the conservation of vertical linear momentum \(\frac{{mv}}{{\sqrt 3 }} - mV\sin \theta = 0\)==>\(\frac{v}{{\sqrt 3 }} = V\sin \theta \)\(...(iv)\)
By solving \((iii)\) and \((iv)\)
\({v^2} + \frac{{{v^2}}}{3} = {V^2}({\sin ^2}\theta + {\cos ^2}\theta )\)
\(⇒\) \(\frac{{4{v^2}}}{3} = {V^2}\) \(⇒\)\(V = \frac{2}{{\sqrt 3 }}v\).

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $m $ દળનો બોલ $v$ વેગથી બીજા તેટલાજ દળના અને વિરૂદ્ધ દિશામાંથી આવતા $2v$ વેગના બોલ સાથે સ્થિતિ સ્થાપક રીતે અથડાય છે. સંઘાત પછી તેઓનો વેગ કેટલો હશે ?View Solution
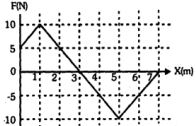
- 2પ્રારંભમાં સ્થિર સ્થિતિ એ રહેલા $m = 2kg$ દળના કણનો બળ $(F)$ વિરૂદ્ધ સ્થાનાંતરણનો આલેખ આકૃતિમાં દર્શાવ્યો છે.View Solution
$(1)$ કણની ઝડપ મહત્તમ $x = ..... m$ અંતરે થશે.
$(2) $ કણની મહત્તમ ઝડપ ...... $ms^{-1}$ છે.
$(3) $ કણ ઝડપ ફરીથી $x = .... m $ સ્થાને શૂન્ય થશે.
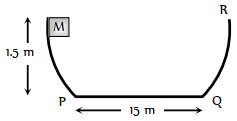
- 3$M $ દળનો પદાર્થ મુકત કરતાં $P$ થી કેટલા ........$m$ અંતરે સ્થિર થશે?પદાર્થ અને સમક્ષિતિજ સપાટી વચ્ચે ઘર્ષણાક $0.2$ છેView Solution
- 4$400\ kg$ની કાર $72 \ kmph$ ની ઝડપથી ગતિ કરે છે.તે તેજ દિશામાં જતાં $4000\ kg$ દળના ટ્રક કે જેની ઝડપ $ 9\ kmph$ છે,તેની સાથે અથડાય છે,અને કાર $18 \ kmph $ ની ઝડપે પાછી ફેંકાય છે,તો અથડામણ પછી ટ્રકની ઝડપ.....$kmph$View Solution
- 5એક લીસી સપાટી પર $0.5\; kg$ દળનો બ્લોક $2 \;ms ^{-1}$ ના વેગથી ગતિ કરી રહ્યો છે. તે બીજા એક $1 \;kg$ દળના પદાર્થ સાથે અથડામણ અનુભવે છે. અથડામણ બાદ બંને પદાર્થ એક સાથે ગતિ કરે છે. આ અથડામણ દરમિયાન ઉર્જાનો વ્યય ($J$ માં) કેટલો થશે ?View Solution
- 6View Solutionવિધાન: ઘર્ષણબળો એ સંરક્ષિ બળો છે.
કારણ: સ્થિતિઉર્જા ને ઘર્ષણબળો સાથે જોડી શકાય.
- 7$m_1$ અને $m_2$ દળના બે સમકડાના ગાડા વચ્ચે એક સ્પ્રિંગ સંકોચાયેલી છે. જ્યારે રમકડાના ગાડાને મુક્ત (છોડવામાં) કરવામાં આવે ત્યારે દરેક ગાડા પર આવેલી સ્પ્રિંગ સમાન સમય $t$ માટે સમાન મૂલ્યનું અને પરસ્પર વિરૂદ્ધ દિશામાં બળ લગાડે છે. જો જમીન અને ગાડા વચ્ચેનો ઘર્ષણ ગુણાંક $\mu$ સમાન હોય તો બે રમકડાના ગાડાઓના સ્થાનાંતરનો ગુણોત્તર શોધો.View Solution
- 8$40 kg$ ના પદાર્થનો વેગ $ 4 m/s$ છે.અને $60 kg$ ના પદાર્થનો વેગ $ 2 m/s $ છે.બંને વચ્ચે અસ્થિતિસ્થાપક સંધાત થાય,તો ગતિઊર્જામાં કેટલા ......... $J$ ઘટાડો થશે?View Solution
- 9$20\,g$ ગોળી $20\,cm$ જેટલી જાડાઈ ધરાવતા બ્લોકને ભેદતા પહેલાનો વેગ $1\,ms^{-1}$ છે, જો બ્લોક $2.5 \times 10^{-2}\,N,$ જેટલો અવરોધ ધરાવતો હોય તો બ્લોકની બહાર આવતા ગોળીનો વેગ કેટલા .............. $\mathrm{ms}^{-1}$ થાય?View Solution
- 10સ્પ્રિંગ તેની મૂળ સ્થિતિમાં છે,$0.25 \,kg$ના દળને મુક્ત કરતા તંત્રએ એ સપાટી પર લગાવેલ મહતમ બળ શોધો? ($N$ માં)View Solution