Angular momentum conservation
\(\mathrm{MV}_{0} \mathrm{L}=\mathrm{MV}_{1}(\mathrm{L}-\ell)\)
\(V_{1}=V_{0}\left(\frac{L}{L-\ell}\right)\)
\(\mathrm{w}_{\mathrm{g}}+\mathrm{w}_{\mathrm{p}}=\Delta \mathrm{KE}\)
\(-m g \ell+w_{p}=\frac{1}{2} m\left(V_{1}^{2}-V_{0}^{2}\right)\)
\(w_{p}=m g \ell+\frac{1}{2} m V_{0}^{2}\left(\left(\frac{L}{L-\ell}\right)^{2}-1\right)\)
\(=m g \ell+\frac{1}{2} m V_{0}^{2}\left(\left(1-\frac{L}{L-\ell}\right)^{-2}-1\right)\)
Now, \(\ell<<\mathrm{L}\)
By, Binomial approximation
\(=m g \ell+\frac{1}{2} m V_{0}^{2}\left(\left(1+\frac{L}{L-\ell}\right)^{-2}-1\right)\)
\(=m g \ell+\frac{1}{2} m V_{0}^{2}\left(\frac{2 \ell}{L}\right)\)
\(\mathrm{W}_{\mathrm{P}}=\mathrm{mg} \ell+\mathrm{mV}_{0}^{2} \frac{\ell}{\mathrm{L}}\)
Here, \(\mathrm{V}_{0}=\) maximum velocity \(=\omega \times \mathrm{A}=(\sqrt{\frac{\mathrm{g}}{\mathrm{L}}})\left(\theta_{0} \mathrm{L}\right)\)
\(\mathrm{So}, \mathrm{w}_{\mathrm{p}}=\mathrm{mg} \ell+\mathrm{m}\left(\theta_{0} \sqrt{\mathrm{gL}}\right)^{2} \frac{\ell}{\mathrm{L}}\)
\(=m g \ell\left(1+\theta_{0}^{2}\right)\)
Download our appand get started for free
Similar Questions
- 1જ્યારે અવમંદન દોલક $100$ દોલનો પૂર્ણ કરે ત્યારે તેનો કંપનવિસ્તાર ઘટીને પ્રારંભિક મૂલ્યના $\frac{1}{3}$ બને છે. જ્યારે તે $200$ દોલનો પૂર્ણ કરે ત્યારે તેનો કંપનવિસ્તાર કેટલો થશે?View Solution
- 2$10$ સેમીનાં કંપવિસ્તાર અને $0.1$ સે. ના આવર્તકાળથી $10$ ગ્રામ દળ ધરાવતો કણ સરળ આવર્તદોલન કરે છે. આ કણ પર લાગતું મહત્તમ બળ (લગભગ) .......... $N$ હશે ?View Solution
- 3કોઈ કણ પોતાની ગતિનું પુનરાવર્તન $8 \,s$ અંતરાલે કરે છે. તો તેની સ્થિતિ ઊર્જા મહત્તમ થયા બાદ ........ $s$ સમયે ફરીથી તેજ મુલ્યે પહોંચશે ?View Solution
- 4બે સરળ આવર્તગતિને નીચે મુજબ આપવામાં આવે છે.View Solution
${y}_{1}=10 \sin \left(3 \pi {t}+\frac{\pi}{3}\right)$
$y_{2}=5(\sin 3 \pi t+\sqrt{3} \cos 3 \pi t)$
${y}_{1}$ અને ${y}_{2}$ ના કંપવિસ્તારનો ગુણોતર ${x}: 1$ હોય તો ${x}$ નું મૂલ્ય કેટલું હશે?
- 5બે સરળ આવર્તગતિ નીચેના સમીકરણ મુજબ આપવામાં આવે છે.View Solution
${x}_{1}=5 \sin \left(2 \pi {t}+\frac{\pi}{4}\right)$ અને ${x}_{2}=5 \sqrt{2}(\sin 2 \pi {t}+\cos 2 \pi {t})$
બીજી ગતિનો કંપવિસ્તાર પહેલી ગતિ કરતાં કેટલા ગણો હશે?
- 6$1 \,m $ લંબાઈવાળું એક સાદુ લોલક $10 \,rad/s$ કોણીય આવૃત્તિથી દોલન કરે છે. લોલકનો આધાર $1 \,rad/s$ જેટલી નાની કોણીય આવૃત્તિ અને $10^{-2}\, m$ જેટલા કંપવિસ્તારથી ઉપર નીચે દોલન કરવાનું શરૂ કરે છે. લોલકની કોણીય આવૃત્તિમાં થતા સાપેક્ષ ફેરફારને _______ દ્વારા સચોટ રીતે દર્શાવી શકાયView Solution
- 7સમક્ષિતિજ સમતલ ઉપર અને નીચે $1\, cm$ કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે. જો તેના પર રહેલો $10\, kg$ દળનો પદાર્થ તેના સંપર્કમાં રહે તે માટે તેની મહત્તમ આવૃતિ($Hz$) કેટલી હોવી જોઈએ?View Solution
- 8${k_1}$ અને ${k_2}$ બળઅચળાંક ઘરાવતી સ્પ્રિંગના છેડે સમાન દળ લગાવવામાં આવે છે. બંને પદાર્થના મહતમ વેગ સમાન છે. તેમના કંપવિસ્તારનો ગુણોતર કેટલો થાય?View Solution
- 9એક સેકન્ડ લોલકની પૃથ્વીની સપાટીથી $h = 2R$ ઊંયાઈએ લંબાઈ $......$ હશે.(જ્યા $R =$ પૃથ્વીની ત્રિજ્યા છે અને પૃથ્વીની સપાટી ઉપર ગુરુત્વાકર્ષણને કારણે પ્રવેગ $\left.g =\pi^2 ms ^{-2}\right)$ છે.View Solution
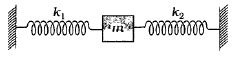
- 10સ્પ્રિંગ અચળાંકો $k _{1}$ અને $k _{2}$ ધરાવતી બે સ્પ્રિંગો એક દળ $m$ સાથે જોડી છે. આ દળનાં દોલનોની આવૃતિ $f$ છે. જો $k _{1}$ અને $k _{2}$ નાં મૂલ્યો ચાર ગણા કરવામાં આવે, તો દોલનોની આવૃત્તિ કેટલી થશે?View Solution