Apply principle of conservation of momentum along \(x-direction,\)
\(mu=mv_1\) \(\cos {45^ \circ } + M{v_2}\cos {45^ \circ }\)
\(mu = \frac{1}{{\sqrt 2 }}\left( {m{v_1} + M{v_2}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\)
Along \(y-direction,\)
\(0 = m{v_1}\sin {45^ \circ } - M{v_2}\sin {45^ \circ }\)
\(0 = \left( {m{v_1} - M{v_2}} \right)\frac{1}{{\sqrt 2 }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)\)
\(m,{u_1} = u\,\,\,\,\,\,M,{u_2} = 0\)
proton Unknown mass After collision
Beforce collision
Coefficient of restution \(e = 1\)
\(\begin{gathered}
= {v_2} - {v_1}\,\cos 90 \hfill \\
\,\,\,\,\,u\,\cos \,45 \hfill \\
\end{gathered} \)
(\(\because \) coillsion is elastic)
\(\begin{gathered}
\Rightarrow \,\frac{{{v_2}}}{{\frac{u}{{\sqrt 2 }}}} = 1 \hfill \\
\Rightarrow \,u = \sqrt 2 {v_{2\,}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {iii} \right) \hfill \\
\end{gathered} \)
Solving eqn\( (i) ,(ii) \& (iii),\) we get mass of unknown patricle, \(M=m\)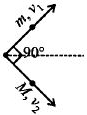
Download our appand get started for free
Similar Questions
- 1$10 m $ ઉંચાઈએથી એક બોલને ફેંક્યા પછી તે અધોદીશામાં $1 m/s $ ના વેગથી ઉતરાણ કરતી લીફટની છત પર અથડાય છે. તો બોલનો પ્રત્યાઘાતી વેગ કેટલા ....$m/s$ હશે ?View Solution
- 2બે સમાન ગોળાઓ $A$ અને $B$ અનુક્રમે $0.5 \;m/s$ તથા $ -0.3 \;m/s $ ના વેગથી એક પરિમાણમાં ગતિ કરતાં સ્થિતિસ્થાપક અથડામણ અનુભવે છે. અથડામણ પછી ગોળા $ B$ અને ગોળા $A$ ના વેગ અનુક્રમે કેટલા થાય?View Solution
- 3$M $ દળનો લાકડાનો બ્લોકને દોરી સાથે બાંઘીને છત પર સ્થિર સ્થિતિએ લટકાવેલ છે. $m$ દળની ગોળી $v $ વેગથી બ્લોકમાં દાખલ થઇને $v/2$ ના વેગથી બહાર આવે છે. જો તેમની ગતિઊર્જામાં કોઈપણ પ્રકારનો વ્યય થતો ન હોય તો બ્લોક કેટલી ઊંચાઇ પર જશે?View Solution
- 4એક $m$ દળવાળી કાર એ એવું એન્જિન ધરાવે છે જે $P$ જેટલો પાવર પૂરો પાડી શકે છે. તો કારએ કેટલાં ન્યૂનતમ સમયમાં સ્થિર સ્થિતિમાંથી $v$ જેટલી ઝડપ સુધી પ્રવેગિત થઈ શકે છે તે...View Solution
- 5ગ્રહની સપાટી પર $5\;m$ ની ઊંચાઈએથી રબરનો દડો છોડવામાં આવે છે, જ્યાં ગુરુત્વાકર્ષી પ્રવેગ જ્ઞાત નથી. બાઉન્સ થયા પછી તે $1.8\;m$ સુધી ઉછળે છે. ઉછાળાવમાં દડો તેનો કેટલા અંશનો વેગ ગુમાવશે?View Solution
- 6$m_1 $ દળનો પદાર્થ $m_2$ દળના સ્થિર પદાર્થ સાથે સંપૂર્ણ સ્થિતિસ્થાપક સંધાત કરે છે.જો ${m_1}$ દળનો વેગ $ 1.5$ માં ભાગનો થાય,તો $\frac{{{m_1}}}{{{m_2}}}$View Solution
- 7View Solutionવિધાન: બે પદાર્થો વચ્ચેના ઝડપી સંઘાત એ ધીમાં સંઘાત કરતાં વધારે ઉગ્ર હોય છે: જ્યારે પ્રારંભિક અને અંતિમ વેગ સમાન હોય ત્યારે પણ.
કારણ: પ્રથમ કિસ્સામાં વેગમાન વધારે હોય છે.
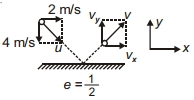
- 8$u$ ઝડપે લીસી અને સમક્ષિતિજ સપાટી સાથે ત્રાંસી અથડામણ અનુભવે છે. જેના $x$ અને $y$ ઘટકો દર્શાવેલ છે. જો રેસ્ટિટ્યુશન ગુણાંક $\frac{1}{2}$ હોય, તો અથડામણ પછીના $x$ અને $y$ ના ઘટકો $v_x$ અને $v_y$ અનુક્રમે ...... હશે ?View Solution
- 9એક સ્પ્રિંગની ખેંચાણ $10$ સે.મી. થી $20$ સે.મી. કરવા માટે તેને ખેંચવા થયેલ કુલ કાર્ય.....View Solution
- 10એક ટ્રક $1200 kg$ નું દળ ઉંચકીને સમતલ રસ્તા પર $10m/s $ ની સ્થાયી ઝડપથી ગતિ કરે છે. જોડાણ વચ્ચેનું તણાવ $1000 N $ છે. દળ પર વપરાતો પાવર ..... હશે. જ્યારે ટ્રક રસ્તા પરના $1m$ ઢાળ અને $6$ મી. ઉંચાઈ વાળા સમતલ પર ગતિ કરે ત્યારે તણાવ ..... હશે.View Solution
