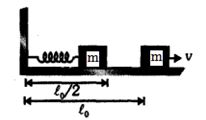
$m$ દળનો એક ટુકડો $k$ સ્પ્રિંગ અચળાંકવાળી એક સ્પ્રિંગ કે જેનો એક છેડો દિવાલ સાથે જોડાયેલ છે તેની વિરૂદ્ધમાં ધકેલાય છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ટુકડો ઘર્ષણરહિત ટેબલ પર સરકે છે. સ્પ્રિંગની પ્રાકૃતિક લંબાઈ $l_0$ છે અને જ્યારે ટુકડો મુક્ત થાય છે ત્યારે તે તેની પ્રાકૃતિક લંબાઈની અડધી લંબાઈ જેટલી સંકોચાય છે તો ટુકડાનો અંતિમ વેગ કેટલો હશે ?

Diffcult
a
પ્રારંભમાં સ્પ્રિંગનું સંકોચન \(\frac{{{\ell _0}}}{2}\) છે. જયારે બ્લોકનું દિવાલથી સ્થાનાંતર \( x \) થાય ત્યારે સંકોચન \((ℓ_0 - x),\) જયાં \(x < ℓ_0\) ઉર્જા સંરક્ષણના નિયમ પરથી,
પ્રારંભમાં સ્પ્રિંગનું સંકોચન \(\frac{{{\ell _0}}}{2}\) છે. જયારે બ્લોકનું દિવાલથી સ્થાનાંતર \( x \) થાય ત્યારે સંકોચન \((ℓ_0 - x),\) જયાં \(x < ℓ_0\) ઉર્જા સંરક્ષણના નિયમ પરથી,
\(\frac{{\text{1}}}{{\text{2}}}\,\,k\,\,{\left( {\frac{{{\ell _0}}}{2}} \right)^2}\,\, = \,\,\frac{1}{2}k\,{\left( {{\ell _0}\,\, - \,\,x} \right)^2}\,\, + \;\,\frac{1}{2}\,\,m{v^2}\)
ઉકેલતા \(v\,\, = \,\,\sqrt {\frac{k}{m}} \,\,{\left[ {\frac{{\ell _0^2}}{4}\,\, - \,\,{{\left( {{\ell _0}\,\, - \,\,x} \right)}^2}} \right]^{1/2}}\)
જ્યારે સ્પ્રિંગ ની તેની પ્રકૃતિક(મૂળ) લંબાઈ મેળવે છે. એટલે કે \(\,x\,\, = \,\,{\ell _0}\,\, \Rightarrow \,\,v\,\, = \,\,\sqrt {\frac{k}{m}} \,\,\frac{{{\ell _0}}}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પદાર્થને ઉપર તરફ ફેંકતાં તેની મહત્તમ ઊંચાઇ $h$ છે.તો$\frac{{3h}}{4},$ઊંચાઇએ ગતિઊર્જા અને સ્થિતિઊર્જાનો ગુણોત્તરView Solution
- 2$4\,g$ અને $16\, g$ ધરાવતાં બે દળોની ગતિ ઊર્જા એક સરખી છે. જે તેમનાં રેખીય વેગમાનનો માનાંકનો ગુણોત્તર $n : 2$ છે. $n$ નું મૂલ્ય ....... હશે.View Solution
- 3કણ પર લાગતું બળ $ F = kx $ છે,જયાં $ k $ ઘન છે,તો સ્થિતિઊર્જાનો આલેખ કયો થશે?View Solution
- 4બે માણસ $A$ અને $B$ પદાર્થને $d$ જેટલું અંતર ખસેડવા માટે તેના પર સ્થાનાંતરની દિશા સાથે અનુક્રમે $45^{\circ}$ અને $60^{\circ}$ ના ખૂણે બળ લગાવીને કાર્ય કરે છે. માણસ $A$ અને માણસ $B$ દ્વારા લાગતા બળનો ગુણોત્તર $\frac{1}{\sqrt{x}}$ છે. તો $x$ નું મૂલ્ય કેટલું હશે?View Solution
- 5View Solutionસ્થિતિઊર્જામાં ઘટાડો કઇ પરિસ્થિતિમાં થાય?
- 6એક સ્થિર કણ બે ભાગોમાં વિભાજિત થાય છે, જેની દળો અનુક્રમે $m_A$ અને $m_B$ છે અને તે અનુક્રમે $v_A$ અને $V_B$ ગતિઓ સાથે ગતિ કરે છે. તેમનાં ગતિ ઊર્જાઓનો ગુણોત્તર $\left(\mathrm{K}_B: \mathrm{K}_{\mathrm{A}}\right)$ કેટલો છે?View Solution
- 7એક પદાર્થને જમીનથી $h$ ઊંચાઈ એ થી મુક્ત કરવામાં આવે છે. જેટલી વાર તે જમીન પર અથડાય ત્યારે તે તેની ગતિઉર્જા ના $50\%$ જેટલી ગતિઉર્જા ગુમાવે છે. તો $t \to \infty $ દરમ્યાન તેણે કાપેલ અંતર કેટલું હશે?View Solution
- 8$4\, kg$, નો પદાર્થ $10\, ms ^{-1}$ ના વેગથી લંબાઈ $8\, m$ અને $100\, Nm ^{-1}$.બળઅચળાંક ધરાવતી સ્પ્રિંગ સાથે અથડાતાં સ્પ્રિંગની લંબાઈ $x\, m$ થાય તો $x$View Solution
- 9$3 \mathrm{~N}$ તણાવ હેઠળ રહેલ સ્થિતિસ્થાપક સ્પ્રિંગ ની લંબાઈ $a$ જેટલી છે. $2 \mathrm{~N}$ તણાવ હેઠળ તેની લંબાઈ $b$ થાય છે. તેની લંબાઈ $(3 a-2 b)$ થાય માટે જરૂરી તણાવ. . . . . . . $\mathrm{N}$થશે.View Solution
- 10એક અચળ $F$ ની અસર હેઠળ સ્થિર અવસ્થાથી શરૂ કરી $m$ દળે એક નિયત અંતર $d$ કાપવા દરમિયાન શરૂ થઈને $l$ જેટલું નિશ્ચિત અંતર કાપવા દરમિયાન $m$ દળે મેળવેલી ગતિ ઉર્જાView Solution
