$m$ દળવાળા અને $e$ વિદ્યુતભાર ધરાવતા ઇલેકટ્રોનને સ્થિર સ્થિતિમાંથી $V$ જેટલા વોલ્ટેજે શૂન્યાવકાશમાં પ્રવેગિત કરવામાં આવે છે, તો ઇલેકટ્રોનનો અંતિમ વેગ કેટલો હશે?
AIPMT 1996, Medium
Download our app for free and get started
a
\(\frac{1}{2} m v^{2}=e V\)
\(\frac{1}{2} m v^{2}=e V\)
final velocity of electron \((v)=\sqrt{\frac{2 e V}{m}}\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$40\, mm$ વ્યાસ ધરાવતી સમાંતર પ્લેટ કેપેસિટરની પ્લેટો વચ્ચે નુ અંતર $(mm)$ શોધો કે જેનું કેપેસીટન્સ $1\; mm$ ત્રિજ્યાના ધાતુ ના ગોળા ના કેપેસિટન્સ જેટલું હોયView Solution
- 2View Solutionવિદ્યુત ડાઈપોલની અક્ષ પરના મધ્યબિંદુ આગળ.......
- 3$X-Y$ યામ પદ્ધતિના ઉગમબિંદુ $(0, 0)$ આગળ $10^{-3}\ \mu C$ નો એક વિદ્યુતભાર મૂકેલો છે. બે બિંદુઓ $A$ અને $B$ $(\sqrt 2 ,\,\,\sqrt 2 )$ અને $(2, 0)$ આગળ ગોઠવેલા છે. બિંદુ $A$ અને $B$ વચ્ચેનો સ્થિતિમાનનો તફાવત .......$V$ હશે.View Solution
- 4બિંદુ $ (x,y,z) $ (મીટરમાં) આગળનું વિદ્યુતસ્થિતિમાન $ V=4x^2$ $volt$ છે. બિંદુ $(1,0,2)$ આગળ વિદ્યુતક્ષેત્રની તીવ્રતા $(V/m$ માં) ......View Solution
- 5View Solutionબે એકસમાન સંઘારકોને(કેપેસીટર) પ્રથમ શ્રેણીમાં અને ત્યારબાદ સમાંતરમાં જોડવામાં આવે છે. આ બે કિસ્સાઓમાં સમતુલ્ય સંઘારક્તાઓનો(કેપેસીટન્સ) ગુણોત્તર .......... હશે.
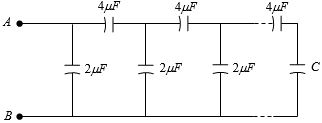
- 6આપેલી આકૃતિમાં $C$ ના ........$\mu F$ મૂલ્ય માટે $A$ અને $B$ વચ્ચેનો સમતુલ્ય કેપેસિટન્સ એ પુનરાવર્તન થતાં વિભાગોની સંખ્યા પર આધાર ન રાખે?View Solution
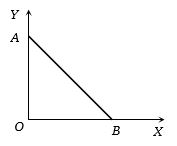
- 7આકૃતિમાં દર્શાવ્યા મુજબ $+q$ વિદ્યુતભારને ઉગમબિંદુ $O$ પર મૂકેલો છે. બિંદુ $A \,(0,a) $ આગળથી $-Q$ વિદ્યુતભારને બિંદુ $B\,(a,0)$ પર સુરેખ માર્ગ $AB$ એ લઇ જવા કેટલું કાર્ય કરવું પડે?View Solution
- 8ગોળાકાર કેપેસિટરની ત્રિજ્યાઓ $0.5\, m$ અને $0.6\, m$ છે. જો ખાલી જગ્યાને $6$ ડાઈ ઈલેકટ્રીક અચળાંકના માધ્યમથી ભરવામાં આવે તો, કેપેસિટરની કેપેસિટિ કેટલી હશે ?View Solution
- 9પ્રદેશમાં $x$ -અક્ષની ઘન દિશામાં સમાન વિદ્યુત આવેલ છે. $A$ ને ઊગમબિંદુ તરીકે લો. $B$ બિંદુ $x$-અક્ષ પર $x = + 1\ cm$ અને $C$ બિંદુ $y$-અક્ષ પર $y = +1\ cm$ અંતર આવેલ છે. તો $A, B$ અને $C$ આગળ સ્થિતિમાનને ....... લાગું પડશે.View Solution
- 10હવાનું આયનીકરણ થયા વગર મહત્તમ વિદ્યુતક્ષેત્ર $10^7\,V/m$ લગાવી શકાય છે. તો $0.10\,m$ ત્રિજયા ધરાવતા ગોળાને હવામાં મહતમ કેટલા વિદ્યુતસ્થિતિમાન સુધી ચાર્જ કરી શકાય?View Solution