મિલ્કનના તેલના ટીપાના પ્રયોગમાં, તેલના ટીપા પર નીચેના પૈકી કયો વિદ્યુતભાર હાજર હોય છે?
Easy
Download our app for free and get started
b
In Millikan's experiment, the charges present on the oil drops are the integral multiples, so \(2 e\) and \(10 e =\left(1.6 \times 10^{-18} C \right)\) charges are present.
In Millikan's experiment, the charges present on the oil drops are the integral multiples, so \(2 e\) and \(10 e =\left(1.6 \times 10^{-18} C \right)\) charges are present.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આપેલ વિસ્તારમાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=\left(\frac{3}{5} E _{0} \hat{i}+\frac{4}{5} E _{0} \hat{j}\right) \frac{ N }{ C }$ વડે આપવામાં આવે છે. $(y-z$ સમતલને સમાંતર) $0.2 \,m^ 2$ ક્ષેત્રફળ ધરાવતી અને $(x-y$ સમતલને સમાંતર) $0.3 \,m^2$ ક્ષેત્રફળ ધરાવતી લંબચોરસ સપાટીમાંથી બતાવેલ ક્ષેત્ર પસાર થતાં મળતા ફ્લક્સનો ગુણોત્તર $a:b$ છે, જ્યાં $a=...........$ છે.View Solution
[ અત્રે $\hat{i}, \hat{j}$ અને $\hat{k}$ એ અનુક્રમે $x, y$ અને $z-$ અક્ષોની દિશામાં એકમ સદિશ છે.]
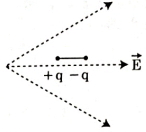
- 2View Solutionઆકૃતિમાં દર્શાવ્યા અનુસાર એક ડાયપોલને વિદ્યુતક્ષેત્રમાં મૂકવામાં આવે છે. તે કઈ દિશામાં ગતિ કરશે?
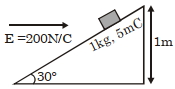
- 3આકૃતિમાં દર્શાવ્યા મુજબ $200 \, \frac{ N }{ C }$ સમાન સમક્ષિતીજ વિદ્યુત ક્ષેત્રમાં મૂકેલ ઢળતી સપાટી, સમક્ષિતીજ સાથે $30^{\circ}$ નો કોણ રચે છે. $1\, kg$ દળ અને $5\, mC$ વિજભાર ધરાવતા પદાર્થને આ ઢળતી સપાટી $1\, m$ ઊંચાઈ વિરામ સ્થાનેથી સરકવા દેવામાં આવે છે. જો ઘર્ષણાંક $0.2$ હોય તો તળીયે પહોંચવા માટે લીધેલો સમય શોધો.($s$ માં)View Solution
$\left[ g =9.8 \,m / s ^{2}, \sin 30^{\circ}=\frac{1}{2}\right.$; $\left.\cos 30^{\circ}=\frac{\sqrt{3}}{2}\right]$
- 4એક વિસ્તારમાં વિદ્યુતક્ષેત્ર એકરૂપ છે. અને $\vec{E}=a \hat{i}+b \hat{j}+c \hat{k}$ વડે આપવામાં આવેલ છે. $\vec{A}=\pi R^2 \hat{i}$ ક્ષેત્રફળની સપાટી સાથે સંકળાયેલ વિદ્યુત ફલક્સ કેટલું છે?View Solution
- 5$Q$ અને $-Q$ વચ્ચેનું અંતર $d\, m$ છે.અને તેમની વચ્ચે લાગતું આકર્ષણ બળ $Fe$ છે.જયારે આ બંને વિદ્યુતભારને $0.3d$ ત્રિજયા ધરાવતા સમાન ગોળા પર મૂકવામાં આવે છે.કે જે બંને ગોળાના કેન્દ્ર વચ્ચેનું અંતર $d$ હોય,તો નવું આકર્ષણ બળView Solution
- 6એક વિદ્યુતભારીત વસ્તુ સાથે સંકળાયેલું વિદ્યુત ફલક્સ $\phi$ છે. આ પદાર્થને હવે ધાતુના પાત્રની અંદર મૂકવામાં આવ્યો છે. પાત્રની બહાર ફલક્સ $\phi$ કેટલું હશે?View Solution
- 7$10\ cm$ ત્રિજયા ધરાવતા ગોળાથી $20\ cm$ અંતરે વિદ્યુતક્ષેત્ર $100\ V/m$ છે.તો કેન્દ્રથી $3\ cm$ અંતરે વિદ્યુતક્ષેત્ર કેટલા .....$V/m$ થાય?View Solution
- 8View Solutionસાચો વિકલ્પ પસંદ કરો.
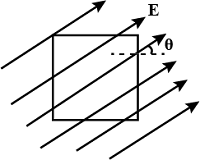
- 9આકૃતિમાં દર્શાવ્યા મુજબ $L$ મીટર બાજુવાળો એક ચોરસ સપાટીને પેપરના સમતલમાં ચોરસની સમક્ષિતિજ બાજુ સાથે $\theta$ ખૂણે $\vec E\;(V/m)$ જેટલા સમાન વિદ્યુતક્ષેત્રમાં મુકેલ છે, તો પૃષ્ઠ સાથે સંકળાયેલ ફલક્સ $volt \;m $ એકમમાં કેટલું થાય?View Solution
- 10$500 \,\mu C$ જેટલા વિદ્યુતભારિત પોલા વાહક કવચ ઉપર $562.5 \,N$ બળ લગાડતાં તેની સપાટી પરની વિદ્યુતક્ષેત્રની તીવ્રતા ......$N/C$ છે.View Solution