$\frac{1}{2}C{l_2}_{(g)}\,\xrightarrow{{\frac{1}{2}{\Delta _{diss}}{H^\Theta }}}\,Cl_{(g)}\,\,\xrightarrow{{{\Delta _{eg}}{H^\Theta }}}\,\,C{l^ - }_{(g)}\,\xrightarrow{{{\Delta _{hyd}}{H^\Theta }}}\,C{l^ - }_{(aq)}$
$({\mkern 1mu} {\Delta _{diss}}{\mkern 1mu} H_{C{l_2}}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} 240{\mkern 1mu} {\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}},{\mkern 1mu} {\mkern 1mu} {\Delta _{eg}}{\mkern 1mu} H_{Cl}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} - 349{\mkern 1mu} {\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}},{\mkern 1mu} {\mkern 1mu} $
${\Delta _{hyd}}H_{C{l^ - }}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} - {\mkern 1mu} 381{\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}})$
પ્રક્રિયા માટે: $\frac{{\text{1}}}{{\text{2}}}C{l_{2(g)}} \to Cl_{(aq)}^ - ;\,\,\Delta H$
$\Delta H = \frac{1}{2}{\Delta _{diss}}\,H_{C{O_2}}^ \circ + {\Delta _{eg}}H_{C{l^ - }}^ \circ + {\Delta _{hyd}}H_{C{l^ - }}^ \circ $
$\frac{1}{2} \times 240 + ( - 349) + ( - 381) = - 610\,kJ\,mo{l^{ - 1}}$
Download our appand get started for free
Similar Questions
- 1$NCl_3$ જેવાં વિસ્ફોટક પદાર્થની $\Delta H_f^o$ નિર્માણ ઉષ્મા ...... થશે.View Solution
- 2$S + \frac{3}{2}{O_2}\, \to \,S{O_3} + 2x\,$ કિલોકેલેરી $\Delta H\,\, = \,\, - y$ કિલોકેલેરી, $S{O_2} + \frac{1}{2}{O_2} \to S{O_3} + y$ કિલોકેલેરી $\Delta H = -2x$ કિલોકેલરી, તો $SO_2$ ની સર્જન ઉષ્મા $= ......$View Solution
- 3અચળ $T$ અને $P$ એ $CO(g) + \frac{1}{2}{O_2}(g) \to C{O_2}(g)$ પ્રકિયા માટે નીચેનામાથી કયું વિધાન સાચું છે ?View Solution
- 4નીચેના કયા એક સમીકરણ માટે $\Delta H^o$ પ્રક્રિયાએ નિપજના $\Delta H_f$ બરાબર હોય છે ?View Solution
- 5$1 \,\,atm$ અને $298\,\, K$ પર આ સંતુલન માટેView Solution
${H_2}O(l)$ $\rightleftharpoons$ ${H_2}O(g)$
- 6પ્રક્રિયા $A + B$ $\rightarrow$ $C + D + q $ જે ઘન એન્ટ્રોપી ફેરફાર ધરાવે છે. તો પ્રક્રિયા........View Solution
- 7$3$ -મીથાઈલબ્યુટિન અને $2$ પેન્ટીન માંટે હાઇડ્રોજનની ઉષ્મા અનુક્રમે $-30\, kcal/mol$ and $-28\,kcal/mol$ છે. $2$ -મિથાઈલબુટેને અને પેન્ટાઇનના દહનની ઉષ્મા છે - અનુક્રમે $784 \,kcal / mol$ અને $-782 \,kcal/mol$ બધા મૂલ્યો પ્રમાણભૂત શરતો હેઠળ આપવામાં આવે છે. તે ધ્યાનમાં લેતા કે બંને આલકેન્સના દહન સમાન નિપજો આપે છે, સમાન પરિસ્થિતિઓમાં નીચેની પ્રક્રિયા માટે $\Delta H$ (in $kcal/mol$) શું છે?View Solution
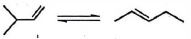
- 8View Solutionઆદર્શ વાયુના પ્રતિવર્તીં સમઉષ્મીય પ્રસરણ દરમ્યાન આંતરિક ઉર્જાનો ફેરફાર......
- 9એક આદર્શવાયુ ના $1$ મોલના $300 \,K$ તાપમાન પર $10$ $atm$ થી $1 \ atm$ સુધીના આદર્શ વાયુના એક મોલ ઉષ્મીય વિસ્તરણ દરમિયાન કરવામાં આવેલું કાર્ય ....... $cal$ (વાયુ અચળાંક $ =2$)View Solution
- 10View Solutionનીચેના વિધાનો વાયુના ઘનની સપાટી પર અધિશોષણ સાથે સંકળાયેલા છે. તે પૈકી અસત્ય વિધાન ઓળખો.
