નીચેના પૈકી કયો વિદ્યુતભાર મિલ્કનના તેલના ટીપાના પ્રયોગમાં હાજર હોતો નથી?
Easy
d
Millikan's oil drop expeniment is used to measure chrorge of an electron.
Millikan's oil drop expeniment is used to measure chrorge of an electron.
We have, \(q=n e \quad \cdots\) where \(n=1,2,3 \cdots\). it was conclucle that, as charge is quantized it should be pritegral multiple of \(1.6 \times 10^{-19}\).
Fon given options,
Excess \(e^{-}=\frac{\text { charge on millikan's oil drop }}{\text { charge on } 1 e^{-}}\)
\(\therefore\) for option \(A\)
Excess \(e^{-}=\frac{4.0 \times 10^{-19}}{1.6 \times 10^{-19}}=2.5\).
for option \(B\)
Excesse \(e^{-}=\frac{6.0 \times 10^{-19}}{1.6 \times 10^{-9}}=3.75\)
for option \(C\)
Excess \(e^{-}=\frac{10.0 \times 10^{-19}}{1.6 \times 10^{-19}}=6.25\)
Here, as all values comes in decimal values and as charge is quantized, we need integral multiple of \(1.6 \times 10^{-19}\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
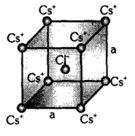
- 1$Cs\, Cl$ ના સામાન્ય સ્ફટકીના બંધારણમાં $Cs^+$ અને $Cl^-$ આયનો $bcc$ રચનામાં આકૃતિમાં દર્શાવ્યા પ્રમાણે ગોઠવાય છે. આઠ $Cs^+$ આયનોને લીધે $Cl^-$ આયન પર લાગતું ચોખ્ખું સ્થિતિ વિદ્યુત શાસ્ત્રનું બળ ....... છે.View Solution
- 2જો બંધ સપાટી પર $\oint_s \vec{E} \cdot \overrightarrow{d S}=0$, તોView Solution
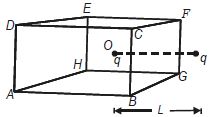
- 3$L$ બાજુવાળા સમઘન $(A\,B\,C\,D\,E\,F\,G\,H)$ ના કેન્દ્ર પર $q$ વિદ્યુતભાર મૂકવામાં આવે છે. કેન્દ્ર $O$ થી $L$ અંતરે $q$ વિદ્યુતભાર મૂકવામાં આવે છે. $BGFC$ માંથી પસાર થતું વિદ્યુતફ્લક્સ કેટલું હશે?View Solution
- 4એક વિદ્યુતભારીત વસ્તુ સાથે સંકળાયેલું વિદ્યુત ફલક્સ $\phi$ છે. આ પદાર્થને હવે ધાતુના પાત્રની અંદર મૂકવામાં આવ્યો છે. પાત્રની બહાર ફલક્સ $\phi$ કેટલું હશે?View Solution
- 5બે સમાન ગોળાઓનો વિદ્યુતભાર $+q$ અને $-q$ છે અને તેઓને અમુક અંતરે મૂકેલા છે. તેમના વચ્ચે $F$ બળ લાગે છે. જો બે ગોળાની વચ્ચે $+q$ વિદ્યુતભાર વાળો સમાન ગોળો મૂકવામાં આવે તો તે બળ અનુભવે છે અને જેનું મૂલ્ય અને દિશા ...... છે.View Solution
- 6ડાઈપોલના મધ્યબિંદુથી અમુક અંતર આગળ એક બિંદુ પર એક વિદ્યુતભાર મૂકેલો છે. જેના પર લાગતું બળ $F$ છે. જો વિદ્યુતભાર બમણા અંતરે વહન પામતો હોય (ગતિ કરતો હોય) તો લાગતું બળ ....... હશે.View Solution
- 7બે વિદ્યુતભાર $9e$ અને $3e$ ને $r$ અંતરે મૂકેલા છે,તો વિદ્યુતક્ષેત્ર શૂન્ય કયા થાય?View Solution
- 8સમાન $m$ દળ અને સમાન વિદ્યુતભાર $q$ ને $16\, cm$ અંતરે રહેલા છે.તે બંને પર લાગતું બળ શૂન્ય હોય,તો $\frac{q}{m} =$ ______View Solution
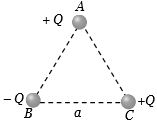
- 9સમબાજુ ત્રિકોણના $A$ બિંદુ પર રહેલાં વિદ્યુતભાર પર $BC$ ને લંબ દિશામાં કેટલું બળ લાગે?View Solution
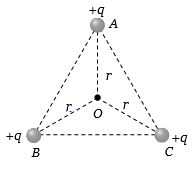
- 10સમબાજુ ત્રિકોણ $ABC$ ના દરેક શિરોબિંદુ પર $ + \,q$ વિજભાર મૂકેલા છે તો $O$ બિંદુ પાસે વિદ્યુતક્ષેત્રની તીવ્રતા કેટલી થાય?View Solution