નીચેની આકૃતિમાં $O$ બિંદુ આગળ ચુંબકીયક્ષેત્રનો ગુણોત્તર કેટલો થાય?
Diffcult
Download our app for free and get started
a
\((a)\) Case \(1\) : \({B_A} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r} \otimes \)
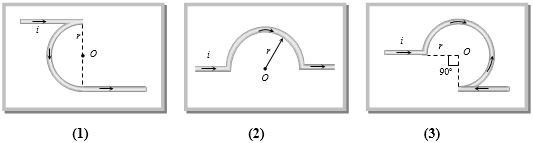
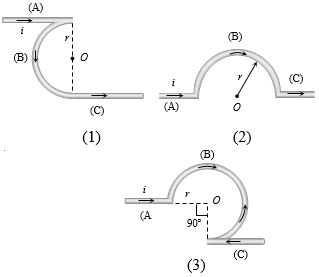
\((a)\) Case \(1\) : \({B_A} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r} \otimes \)
\({B_B} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}\) \(\odot \)
\({B_C} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}\) \(\odot \)
\({B_1} = {B_B} - ({B_A} + {B_C})\) \(⇒\) \({B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi i}}{r}\) \(\odot \) \(..... (i) \)
Case \(2\) : \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi i}}{r} \otimes \) \(.....(ii) \)
Case \(3\) : \({B_A} = 0\)
\({B_B} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{(2\pi - \pi /2)}}{r} \otimes \) \( = \frac{{{\mu _0}}}{{4\pi }}.\frac{{3\pi i}}{{2r}} \otimes \)
\({B_C} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}\) \(\odot\)
\({B_3} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}\left( {\frac{{3\pi }}{2} - 1} \right) \otimes \) \( ....(iii)\)
\({B_1}:{B_2}:{B_3} = \pi \) \( \odot : \pi \odot : \) \(\left( {\frac{{3\pi }}{2} - 1} \right) \otimes \) \( = - \frac{\pi }{2}:\frac{\pi }{2}:\left( {\frac{{3\pi }}{4} - \frac{1}{2}} \right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
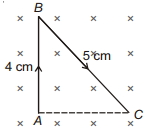
- 1એક એકરૂપ સુવાહક તાર $A B C$ નું દળ $10\,g$ છે. તેમાંથી $2\,A$નો વિદ્યુતપ્રવાહ પસાર થાય છે. તારને એક્સમાન ચુંબકીય ક્ષેત્ર $B=2\,T$ માં રાખેલ છે. તારનો વેગ ........... $ms ^{-2}$ હશે.View Solution
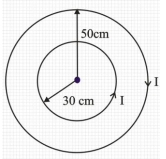
- 2આપેલ આકૃતિમાં દર્શાવ્યા અનુસાર $r _1=30\,cm$ અને $r _2=50\,cm$ ત્રિજ્યા ધરાવતી બે વર્તુળાકાર સમકેન્દ્રીય ગોળાઓને $X-Y$ સમતલમાં મૂકવામાં આવ્યા છે. આકૃતિમાં દર્શાવ્યા અનુસાર તેમાંથી $I=7\,A$ જેટલો વીજપ્રવાહ પસાર કરવામાં આવે છે. આ બે વર્તુળાકાર ગાળાઓથી બનતા તંત્રની સમાસ ચુંબકીય ચાકમાત્રા $..............$ થશે.View Solution
- 3View Solutionબે સમાન લંબાઇના તારમાંથી ચોરસ અને વર્તુળ બનાવવામાં આવે છે.બંનેમાં સમાન પ્રવાહ પસાર કરતાં ચુંબકીય ચાકમાત્રાનો ગુણોત્તર કેટલો થાય?
- 4$L$ લંબાઇ અને $I$ પ્રવાહધારિત તારને વર્તુળમાં વાળતાં ચુંબકીય મોમેન્ટ કેટલું થાય?View Solution
- 5$4.5 \times 10^{5} \;m / s$ના વેગથી ગતિ કરતાં બિંદુવત વિજભારના કારણે ઉત્પન્ન થતાં વિદ્યુતક્ષેત્ર અને ચુંબકીયક્ષેત્રનો ગુણોતર કેટલો થાય?View Solution
- 6$25\,cm ^2$ નું ક્ષેત્રફળ ધરાવતા એક ચોરસગાળાનો અવરોધ $10\,\Omega$ છે. ગાળાને $40.0\,T$ ધરાવતા નિયમિત ચુંબકીય ક્ષેત્રમાં મૂકવામાં આવેલ છે. ગાળાનું સમતલ ચુંબકીયક્ષેત્રને લંબ છે. ગાળાને $1.0$ સેકન્ડના ગાળામાં ધીમે-ધીમે ચુંબકીયક્ષેત્રમાંથી બહાર કાઢવા માટે થતું કાર્ય $..........\times 10^{-3}$ હશે.View Solution
- 7View Solutionપ્રવાહ ધારીત લાંબા તારની નજીક એક ઋણ વિજભાર ગતિ કરે છે. આ વિજભાર પર લાગતું બળ તારના પ્રવાહની દિશાને સમાંતર છે. તો વિજભાર કઈ રીતે ગતિ કરતો હશે?
- 8ગેલ્વેનોમીટરના સ્કેલ માપને $25 $ સમાન વિભાગ પાડવામાં આવે છે.ગેલ્વેનોમીટરનો અવરોધ $100 \,\Omega$ છે.ગેલ્વેનોમીટરની વિધુત સંવેદિતા $ 4 × 10^{-4} \,A/div.$ છે.ગેલ્વેનોમીટર $2.5 \,volt$ માપવા માટે કેટલા .................... $ohm$ અવરોધ શ્રેણીમાં જોડવો પડે?View Solution
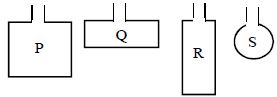
- 9$2.0\,m$ લંબાઈના ચાર તારમાંથી $P,\,Q,\,R$ અને $S$ લૂપ બનાવવામાં આવે છે.તેને નિયમિત ચુંબકીયક્ષેત્રમાં મૂકવામાં આવે છે.તેમાંથી સમાન પ્રવાહ પસાર કરતા કઈ લૂપ પર મહતમ ટોર્ક લાગશે.View Solution
- 10નીચે બે વિધાનો આપેલા છે.View Solution
વિધન $I:$ ચલિત ગૂંચળાવાળા ગેલ્વેનોમીટરમાં ગૂંચળાના આંટાની સંખ્યા બમણી કરતાં તેની પ્રવાહ સંવેદિતા બમણી થાય.
વિધન $II$ : ફક્ત ગૂંચળાના આંટાની સંખ્યા વધારીને ચલિત ગૂંયળાવાળા ગેલ્વેનીમીટર પ્રવાહ સંવેદિતા વધારતા તેની વોલ્ટેજ સંવેદિતા પણ તેટલા જ ગુણોત્તર પ્રમાણે વધશે.
ઉપર્યુક્ત કથનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરો.