નીચેની માહિતી પરથી ઇથિલિનની સર્જન એન્થાલ્પી.......$kJ\,mo{l^{ - 1}}$ ગણો.
${C_{\left( {graphite} \right)}} + {O_{2\left( g \right)}} \to C{O_{2\left( g \right)}}\,;\Delta H = - 393.5\,kJ$
${H_{2\left( g \right)}} + 1/2{O_{2\left( g \right)}} \to {H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 286.2\,kJ$
${C_2}{H_{4\left( g \right)}} + 3{O_{2\left( g \right)}} \to 2C{O_{2\left( g \right)}} + 2{H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 1410.8\,kJ$
Medium
Download our app for free and get started
c
\(i)\) \(C + O _2 \longrightarrow CO _2 \quad \Delta H _{ i }=-393.5\)
\(i)\) \(C + O _2 \longrightarrow CO _2 \quad \Delta H _{ i }=-393.5\)
\(ii)\) \(H _2+\frac{1}{2} O _2 \rightarrow H _2 O \quad \Delta H _{i i }=-286.2\)
\(iii)\) \(C _2 H _4+3 O _2 \longrightarrow 2 CO _2+2 H _2 O \quad \Delta H _{\text {iil }}=-1410.8\)
\(iv)\) \(2 C +2 H _2 \longrightarrow C _2 H _4 \Delta H = (?)\)
\(iv)\) \(=2 (i) - (ii) +2 (iii)\)
\(\therefore \Delta H =2 \Delta H _1+2 \Delta H _{ii}-2 \Delta H _{\text {iii}}\)
\(=2(-393.5)-2(-286.2)-(-1410.8)\)
\(=-787+572.4+1410.8\)
\(=-1359.4+1410.8\)
\(=+51.4\, kJ\, mol^{-1}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનીચેનામાંથી કઈ એક પ્રણાલીનો માત્રાત્મક ગુણધર્મ ધરાવે છે ?
- 2View Solutionસમોષ્મી પ્રક્રિયા માટે નીચેનામાંથી કયો સંબંધ સાચો છે ?
- 3$NH_4OH$ ની $HCl$ સાથેની તટસ્થીકરણ એન્થાલ્પી $-51 .46\,kJ\,mol^{-1}$ અને $NaOH$ ની $HCl$ સાથેની તટસ્થીકરણ એન્થાલ્પી $-55. 90\,kJ\,mol^{-1}.$ છે. તો $NH_4OH$ ની આયનીકરણ ઊર્જા ......$kJ\,mol^{-1}$View Solution
- 4$q = - w$ ....... માટે સાચુ નથી.View Solution
- 5$\,2C\,\, + \,\,2{O_2}\, \to \,\,2C{O_2}\,:\,\,\Delta \,H\,\, = \,\, - 787$ કિલોજૂલ ${H_2} + \frac{1}{2}{O_2} \to {H_2}O\,\,:\,\,\Delta H\,\, = \,\, - 286\,$ કિલોજૂલ અને ${C_2}{H_2} + \frac{5}{2}{O_2} \to 2C{O_2} + {H_2}O\,\,:\,\,\Delta H\,\, = \,\, - 1310\,$ કિલોજૂલ તો એસિટિલીનની સર્જન ઉષ્મા =........કિલોજૂલView Solution
- 6આપેલ આક્રૂતિને ધ્યાનમાં લો.View Solution
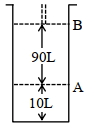
$18^{\circ} \mathrm{C}$ પર, સ્થાન $A$ પર, પિસ્ટન સાથે જોડેલા (fitted) સિલિન્ડર માં આદર્શ વાયુનો $1$ $\mathrm{mol}$ રાખેલ છે. જો તાપમાન માં કોઈપણ જાતનો ફેરફાર ન કરીએ તો પિસ્ટન એ સ્થાન $B$ તરફ ખસે છે ત્યારે આ પ્રતિવર્તી પ્રક્રમ માં થયેલ કાર્ય $'x' L atm$ છે. $x=-$ ........... $L.atm$ (નજીક નો પૂર્ણાક)
[આપેલ : નિરપેક્ષ તાપમાન $={ }^{\circ} \mathrm{C}+273.15, \mathrm{R}=0.08206 \mathrm{~L} \mathrm{~atm} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$ ]
- 7$A _2+ B _2 \rightarrow 2 AB . \Delta H_f^0=-200\,kJ\,mol ^{-1} AB , A _2$ અને $B _2$ એ દ્રીપરમાણ્વિક અણુઓ છે. $A _2, B _2$ અને $AB$ બી બંંધ એન્થાલ્પીઓ $1:0.5:1$ના ગુણોત્તરમાં હોય તો, તો પછી $A _2$ ની બંંધ એન્થાલ્પી $.........\,kJ\,mol ^{-1}$ (નજીકનો પૂર્ણાક)View Solution
- 8કાલ્પનિક પ્રક્રિયા $A_2$ $_{(g)} +$ $B_2$$_{(g)}$ $\rightleftharpoons$ $2AB_{(g)}$ માટે $200 \,K$ એ $\Delta rG$ અને $\Delta rS$ અનુક્રમે $20\, kJ/mole$ and $-20\, JK^{-1}\, mol^{-1}$ અને $\Delta rGr$ અને $\Delta Sr$ અનુક્રમે $20 \,kJ/mole$ અને $-20\, JK ^{-1}$ $mol^{-1}$ છે. જો $\Delta CP. 20 \,JK^{-1} \,mol^{-1}$ હોય તો $4004\,K$ એ $\Delta H_r$ શોધો.......$kJ/mole$View Solution
- 9$S + O_2 \rightarrow SO_2 : \Delta H_1 = -298.2$ કિલોજૂલ, $SO_2 + 1/2\, O_2 \rightarrow SO_3 : \Delta H_2 = -98.7$ કિલોજૂલ $SO_3 + H_2O \rightarrow H_2SO_4 : \Delta H_3 = {-1}30.2$ કિલોજૂલ અને $H_2 + 1/2\, O_2 \rightarrow H_2O : \Delta H_4 = -287.3$ કિલોજૂલ, તો $H_2SO_4$ ની સર્જન ઉષ્મા $= ?$ ...... કિલોજૂલView Solution
- 10આંતરિક ઊર્જા ફેરફાર જ્યારે પ્રણાલી અવસ્થા $A$ થી $B$ સુધી જાય છે ત્યારે $ 40 \, \, kJ/mole $ છે. જો પ્રણાલી પ્રતિવર્તી માર્ગ દ્વારા $A$ થી $B$ સુધી જાય અને અપ્રતિવર્તી માર્ગ દ્વારા $A$ અવસ્થામાં પરત આવે તો આંતરિક ઊર્જામાં ચોખ્ખો ફેરફાર શું થશે?View Solution