નજીક દેખાતા બે તારા $(Stars)$ નું અંતર માપવા માટે પરિચ્છેદ $2.3.1$ ની દૃષ્ટિસ્થાનભેદની રીતના સિદ્ધાંતનો ઉપયોગ કરવામાં આવે છે. સૂર્યની આસપાસ પોતાની ભ્રમણ કક્ષામાં છ મહિનાના સમય અંતરાલમાં પૃથ્વીનાં બે સ્થાનોને જોડતી આધાર રેખા $AB$ છે એટલે કે આધાર રેખા પૃથ્વીની કક્ષાના વ્યાસ $\approx 3 \times 10^{11}\;m$ જેટલી લગભગ છે. જોકે નજીક રહેલા બે તારા એટલા દૂર છે કે આટલી લાંબી આધાર રેખા હોવા છતાં તેઓ $1”$ (સેકન્ડ) જેટલો ચાપનો $(Arc)$ દૃષ્ટિસ્થાનભેદ દર્શાવે છે. ખગોળીય સ્તર પર લંબાઈનો સુવિધાજનક એકમ પાર્સેક છે. પાર્સેક કોઈ પદાર્થનું અંતર સૂચવે છે કે જે પૃથ્વી અને સૂર્ય વચ્ચેનાં અંતર જેટલી આધાર રેખાના બે છેડાઓએ આંતરેલ ખૂણો $1”$ $(Second \,Arc)$ બરાબર હોય. એક પાર્સેકનું મૂલ્ય મીટરમાં કેટલું થશે ?
Easy
d
Diameter of Earth's orbit \(=3 \times 10^{11} m\)
Diameter of Earth's orbit \(=3 \times 10^{11} m\)
Radius of Earth's orbit, \(r=1.5 \times 10^{11} m\)
Let the distance parallax angle be \(1^{\prime \prime}=4.847 \times 10^{-6}\) rad.
Let the distance of the star be \(D\)
Parsec is defined as the distance at which the average radius of the Earth's orbit subtends an angle of \(1^{\pi}\) \(\therefore\) We have \(\quad \theta=\frac{r}{D}\)
\(D=\frac{r}{\theta}=\frac{1.5 \times 10^{11}}{4.847 \times 10^{-6}}\)
\(=0.309 \times 10^{-6} \approx 3.09 \times 10^{16} m\)
Hence, \(1 parsec \approx 3.09 \times 10^{16}\; m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પારિમાણીક સામ્યતા (સમાનતા)ના સિદ્ધાંત અનુસાર નીચેનામાંથી કયું સાયું છે તે દર્શાવો.જ્યાં $T$ એ આવર્તકાળ, $G$ એ ગુરુત્વકર્ષી અયળાંક, $M$ દળ અન $r$ એ કક્ષાની ત્રિજ્યા છે.View Solution
- 2પતરા પર લાગતા બળ અને તેની બાજુઓની લંબાઈની મદદથી ચોરસ પતરા પરનું દબાણ માપેવામાં આવે છે, જો બળ અને લંબાઈના માપનમાં મહત્તમ ત્રુટિ અનુક્રમે $4\%$ અને $2\%$ હોય તો દબાણના માપનમાં મહત્તમ ત્રુટિ ........ $\%$ હશે .View Solution
- 3$6.28$ સેમી. લાંબા રેસાની લંબાઈનું સૌથી યોક્કસ અવલોકન ....... $cm$ છે?View Solution
- 4ભૌતિક રાશિનો $SI$ એકમ પાસ્કલ-સેકન્ડ છે. આ રાશિનું પારિમાણીક સૂત્ર ........... થશે.View Solution
- 5બે ભૌતિક રાશિ $A$ અને $B$ ના પારિમાણીક સૂત્રો અલગ હોય,તો નીચેનામાંથી કયું પારિમાણિક દ્રષ્ટિએ સત્ય છે.View Solution
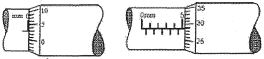
- 6સ્ક્રૂગેજની આકૃતિ આપેલ છે. આકૃતિ $(i)$ માં સ્ક્રૂગેજ જ્યારે બંધ કરેલ હોય ત્યારની શૂન્ય ત્રુટિ દર્શાવેલ છે. આકૃતિ $(ii)$ માં બોલ બેરિંગના વ્યાસ માપવા માટે લીધેળ અવલોકન માટેની સ્ક્રૂગેજની આકૃતિ છે. તો બોલ બેરિંગનો વ્યાસ ($mm$ માં) કેટલો હશે? વર્તુળાકાર સ્કેલમાં $50$ કાંપા છે.View Solution
- 7$C$ અને $L$ અનુક્રમે કેપેસિટન્સ અને ઇન્ડકટન્સ હોય તો $LC$ નું પારિમાણિક સૂત્ર શું થાય?View Solution
- 8$6.28$ સેમી. લાંબા રેસાની લંબાઈનું સૌથી યોક્કસ અવલોકન ....... $cm$ છે?View Solution
- 9દળના માપનમાં અને ઝડપના માપનમાં પ્રતિશત ત્રુટિ અનુક્રમે $3\%$ અને $2\%$ ની હોય,તો ગતિઊર્જામાં મહતમ પ્રતિશત ત્રુટિ ......... $\%$ થશે.View Solution
- 10$r.m.s.$ (root mean square) વેગનું પારિમાણિક સૂત્ર શું થાય?View Solution
