નળાકાર કેપેસીટર વિદ્યુતભાર $'Q'$ તથા લંબાઇ $'L'$ ધરાવે છે જો લંબાઇ તથા વિદ્યુતભાર બંને બમણા કરવામાં આવે તો (બાકીની રાશી સમાન રાખીને) કેપેસીટરમાં સંગ્રહીત ઉર્જા.....
Easy
Download our app for free and get started
b
નળાકાર કેપેસીટરનું કેપેસીટન્સ \( = \,\,\frac{{2\pi {\varepsilon _0}L}}{{In\,(b\,/\,a)}}\)
નળાકાર કેપેસીટરનું કેપેસીટન્સ \( = \,\,\frac{{2\pi {\varepsilon _0}L}}{{In\,(b\,/\,a)}}\)
કેપેસીટરમાં સંગ્રહાયેલી ઉર્જા \(\frac{1}{2}\,\frac{{{Q^2}}}{C}\,\, = \,\,\frac{1}{2}\,\frac{{{Q^2}In\,(b\,/\,a)}}{{2\pi {\varepsilon _0}L}}\,\, = \) [અચળ] \( = \,\,\,\frac{{{Q^2}}}{L};\)
જો વિદ્યુતભાર બમણો અને લંબાઈ બમણી કરવામાં આવે તો [અચળ] \(\frac{{Q{'^2}}}{{L'}}\,\, = \,\,\frac{4}{2}\left( {\frac{{{Q^2}}}{L}} \right)\,\, = \,\,2\) ગણી ઉર્જા
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસ્થિતિમાન દર્શક (potential gradient) એ કેવી રાશી છે ?
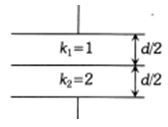
- 2$A$ ક્ષેત્રફળ ધરાવતી બે સમાંતર પ્લેટોને બે જુદા જુદા ડાઇઇલેક્ટ્રીક થી છુટી પાડેલ છે તો પરીણામી કેપેસીટન્સ શોધો.View Solution
- 3$10^{3 }\ m$ વ્યાસ ધરાવતો ધાતુ ગોળાના સ્વરૂપમાં એક રેડિયો એકટિવ પદાર્થ પ્રતિ સેકન્ડે $6.25 \times 10^{10}$ કણોના અચળ દરે કણોનું ઉત્સર્જન કરે છે. જો વાહક વિદ્યુતીય રીતે અલગ કરેલો હોય, તો તેનો સ્થિતિમાન $1.0$ વોલ્ટ, વધારવા માટે કેટલો સમય લેશે? $80\%$ ઉત્સર્જિત કણો સપાટી પરથી બહાર નીકળે છે. તેમ ધારો.......$\mu s$View Solution
- 4ઉગમબિંદુ પર એક બિંદુવત ડાયપોલ $\vec p = - {p_0}\hat x$ છે. ડાયપોલના કારણે $y-$ અક્ષ પર $d$ અંતરે વિદ્યુતસ્થિતિમાન અને વિદ્યુતક્ષેત્ર અનુક્રમે કેટલું થશે?(અનંત અંતરે $V = 0$)View Solution
- 5વિદ્યુતભારીત કેપેસિટરની પ્લેટો વચ્ચેની સરેરાશ વિદ્યુતીય ઊર્જા ઘનતા (અહી $q$ = કેપેસિટર પર વિદ્યુતભાર અને $A$= કેપેસિટરની પ્લેટોનું ક્ષેત્રફળ)View Solution
- 6$C_1=1\,\mu F$ કેપેસિટર મહત્તમ $V_1=6\,kV$ નો વોલ્ટ અને $C_2=3\,\mu F$ કેપેસિટર મહત્તમ $V_2=4\,kV$ નો વોલ્ટ સહન કરી શકે છે.હવે,આ બંને કેપેસિટરને શ્રેણીમાં જોડીને કેટલો મહત્તમ વોલ્ટેજ ......$kV$ આપી શકાય?View Solution
- 7બે પ્લેટો વડે સમાંતર પ્લેટ કેપેસિટર રચેલ છે. દરેક પ્લેટનું ક્ષેત્રફળ $100\ cm^2, \,1\ mm$ અંતરે અલગ કરેલી છે. એક $5.0$ ડાઈ ઈલેકટ્રીક અચળાંંક ધરાવતા ડાઈ ઈલેકટ્રીક અને ડાઈ ઈલેકટ્રીક સ્ટ્રેન્થ $1.9 \times 10^7\ V/m$ પ્લેટોની વચ્ચે ભરવામાં આવે છે. ડાઈ ઈલેકટ્રીક બ્રેક ડાઉન કર્યા સિવાય કેપેસિટર પર સંગ્રહ કરી શકાતો મહત્તમ વિદ્યુતભાર શોધો.View Solution
- 8બે સમાંતર પ્લેટોવાળા કેપેસીટરોની પ્લેટોના ક્ષેત્રફળ અનુક્રમે $100\,cm ^2$ અને $500\,cm ^2$ છે. જો તેમને સમાન વિદ્યુતભાર અને સમાન સ્થિતિઓને રખાય અને તેમની પ્લેટો વચ્ચેનું અંતર પણ પ્રથમ પ્લેટ પર $0.5\, mm$ હોય, તો બીજા કેપેસીટર પરની પ્લેટો વચ્ચેનું અંતર $.......\,cm$ હશે.View Solution
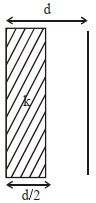
- 9એક સમાંતર પ્લેટ સંઘારક (કેપેસીટર) સંરચનામાં, સંઘારકની પ્લેટનું ક્ષેત્રફળ $2 \,m ^{2}$ અને તેમની વચ્ચેનું અંતર $1\, m$ છે. જો પ્લેટો વચ્ચેની જગ્યા $0.5\, m$ જાડાઈ અને $2\, m ^{2}$ ક્ષેત્રફળ ધરાવતા (આકૃત્તિ જુઓ) ડાયઈલેક્ટ્રિક (અવાહક) પદાર્થ દ્વારા ભરવામાં આવે તો આ સંરચનાની સંઘારતા (કેપેસીટન્સ) ...... .........$\, \varepsilon_{0}$ થશે.View Solution
(પદાર્થનો ડાયઈલેક્ટ્રીક અચળાંક $=3.2$) (નજીકત્તમ પૂર્ણાંકમાં ગણો)
- 10View Solutionએક કેપેસિટરને ચાર્જ કરીને હવે, બેટરી દૂર કરવામાં આવે છે અને એક ડાઈ ઈલેકટ્રીક પ્લેટ છે દાખલ કરવામાં આવે તો સાચુ વિધાન પસંદ કરો.