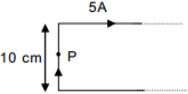
$P$ પાસે એકમ લંબાઈ દીઠ બળ શોધો.
AIIMS 2019, Medium
Download our app for free and get started
b
The magnetic field at \(B\),
The magnetic field at \(B\),
\(B=\frac{\mu_{0} i}{4 \pi r}+0+\frac{\mu_{0} i}{4 \pi r}\)
\(=\frac{\mu_{0} \times 5}{4 \pi \times 5 \times 10^{-2}} \times 2\)
\(=\frac{\mu_{0}}{4 \pi} \times 200\)
\(=2 \times 10^{-5} T\)
Consider the length of wire element at \(P\) is \(dl\).
The force per unit length at \(P\) is,
\(F=i B d l\)
\(\frac{F}{d l}=i B\)
\(=5 \times 2 \times 10^{-5}\)
\(=10^{-4} N / m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$20\, turns/cm$ ધરાવતા સોલેનોઇડમાં $20\, millitesla$ ચુંબકીયક્ષેત્ર ઉત્પન્ન કરવા માટે કેટલો પ્રવાહ પસાર કરવો પડે?.......$A$ $\left( {\frac{{{\mu _0}}}{{4\pi }} = {{10}^{ - 7}}\,Tesla{\rm{ - }}metre\,/\,ampere} \right)$View Solution
- 2View Solutionએક આંટાવાળી કોઇલ ચોક્કસ લંબાઈના તારમાંથી બને છે અને પછી તે જ લંબાઈથી બે આંટાવાળી કોઇલ બનાવવામાં આવે છે. જો બંને કિસ્સાઓમાં સમાન પ્રવાહ પસાર થાય છે, તો તેમના કેન્દ્રો પર ચુંબકીય પ્રેરણનો ગુણોત્તર કેટલો થશે?
- 3$R$ ત્રિજયાની રીંગના કેન્દ્ર આગળ અને કેન્દ્રથી $3R$ અંતરે અક્ષ પરના બિંદુએ ચુંબકીયક્ષેત્રનો ગુણોતર કેટલો થાય?View Solution
- 4$4 \pi$ મીટર લંબાઈના તારને વાળીને $6$ બાજુઓ વાળો બહુકોણ (ષટ્કોણ) બનાવવામાં આવે છે. જો બહુકોણ $4 \pi \sqrt{3} \mathrm{~A}$ વિદ્યુત્પવાહનું વહન કરતો હોય તો બહુકોણના કેન્દ્ર પરનું ચુંબકીય ક્ષેત્ર $10^{-7} x$ ટેસ્લા છે. $x$ નું મૂલ્ય____________છે.View Solution
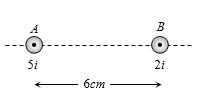
- 5$'B' $ તારથી કેટલા અંતરે ચુંબકીયક્ષેત્ર શૂન્ય થાય?View Solution
- 6View Solutionજો સમાન વેગમાન ધરાવતો ઇલેક્ટ્રોન અને પ્રોટોન ચુંબકીયક્ષેત્રને લંબ પ્રવેશે, તો ...
- 7View Solutionસાચું વિધાન પસંદ કરો.
- 8$12\, A$ પ્રવાહધારીત તારથી કેટલા અંતરે ચુંબકીયક્ષેત્ર $3 \times 10^{-5} Wb / m ^{2}$ થાય?View Solution
- 9ગેલ્વેનોમીટરના કોઇલનો અવરોઘ $100\,\Omega$ છે અને તે $30\,mA $ ના પ્રવાહ માટે પૂર્ણ સ્કેલ આવર્તન દર્શાવે છે.તેને $30 \,V $ માપીશકે તેવા વોલ્ટમીટર તરીકે કાર્ય કરવવા કેટલો અવરોધ($\Omega$) જોડાવો પડે?View Solution
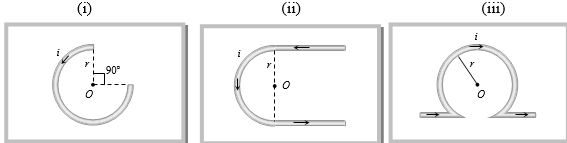
- 10આપેલ પરિપથ માટે $O $ બિંદુ પાસે ચુંબકીયક્ષેત્ર આપેલ છે તો નીચે પૈકી કયું સાચું થાય?View Solution
$(i)$ $(ii)$ $(iii)$ (A) $\frac{{{\mu _0}i}}{2r}$ $\odot$ (A) $\frac{{{\mu _0}}}{{2\pi }}\frac{i}{r}(\pi - 2)$ (A) $\frac{{{\mu _0}}}{{2r}}\frac{{2i}}{r}(\pi + 1)$ $\otimes$ (B) $\frac{{{\mu _0}i}}{{2r}}$ $\otimes$ (B) $\frac{{{\mu _0}i}}{{4\pi }}.\frac{i}{r}(\pi + 2)$ $\otimes$ (B) $\frac{{{\mu _0}i}}{{4r}}.\frac{{2i}}{r}(\pi - 1) \otimes $ (C) $\frac{{{3\mu _0}i}}{{8r}}$ $\otimes$ (C) $\frac{{{\mu _0}i}}{4r}$ $\otimes$ (C) $Zero$ (D) $\frac{{{3\mu _0}i}} {{8r}}$ $\odot$ (D) $\frac{{{\mu _0}i}}{4r}$ $\odot$ (D) $Infinite$ 