પારના $64$ સૂક્ષ્મ ટીપાંઓ કે જે દરેકની ત્રિજ્યા $'r'$ અને વિદ્યુતભાર $q$ ભેગા મળીને એક અને મોટા મોટું ટીપું બનાવે છે. દરેક સૂક્ષ્મ ટીપાના વિદ્યુતભારની પૃષ્ઠ ઘનતાનો ગુણોત્તર ........ છે.
Medium
b
Given that,
Given that,
Droplets of mercury \(=64\)
Density of small droplet \(=\sigma_{\text {small }}\)
Density of big droplet \(=\sigma_{\text {biz }}\)
We know that,
\(\frac{\sigma_{\text {small }}}{\sigma_{\text {big }}}=\frac{ q }{ Q } \times \frac{ R ^2}{ r ^2}\)
\(\frac{\sigma_{\text {small }}}{\sigma_{\text {big }}}=\frac{q}{(n q)} \times \frac{\left( n ^{\frac{1}{3}} r \right)}{ r ^2}\)
\(\frac{\sigma_{\text {small }}}{\sigma_{\text {big }}}= n ^{-\frac{1}{3}}\)
Now, put the value of \(n\)
\(\frac{\sigma_{\text {small }}}{\sigma_{\text {big }}}=(64)^{-\frac{1}{3}}\)
\(\frac{\sigma_{\text {small }}}{\sigma_{\text {big }}}=\frac{1}{4}\)
Hence, the ratio is \(\frac{1}{4}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$-10$ વોલ્ટ જેટલું સ્ચિતિમાન ધરાવતાં એક બિંદુ $V$ જેટલું સ્થિતિમાન ધરાવતાં એક બિંદુ પર $2C$ જેટલો ચાર્જને લાવવા માટે $50$ જુલ જેટલું કાર્ય કરવું પડતું હોય તો $V$ નું મુલ્ય $....$View Solution
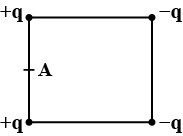
- 2આકૃતિમાં દર્શાવ્યા મુજબ $2L$ લંબાઇના ચોરસનાં શિરોબિંદુઓ પર $ +q,+q,-q $ અને $-q$ વિદ્યુતભારો મૂકેલા છે, $+q $ અને $-q$ વિદ્યુતભારોના મઘ્યબિંદુ $ A$ આગળ વિદ્યુતસ્થિતિમાન કેટલું મળે?View Solution
- 3$25\,\mu \,F$ ના ચાર કેપેસીટરને આકૃતિમાં દર્શાવ્યા મુજબ જોડેલા છે. જો $dc$ વોલ્ટમીટરનું અવલોકન $200\,V$ હોય તો કેપેસીટરની દરેક પ્લેટ પરનો વિદ્યુતભાર કેટલો હશે?View Solution
- 4ચાર વિદ્યુતભારો $+Q, -Q, +Q$ અને $-Q$ ચોરસના ચાર ખૂણાઓ પર મૂકેલા છે. તો ચોરસના કેન્દ્ર આગળ......View Solution
- 5View Solutionવિદ્યુતભારિત વાહક ગોળા માટે કયું વિધાન સાચું નથી?
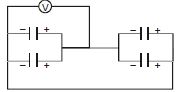
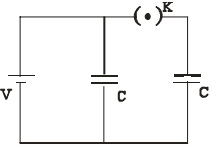
- 6દર્શાવ્યા અનુસાર $V$ જેટલો સ્થિતિમાનનો તફાવત ધરાવતા ઉદગમને બે એક સમાન સંધારકો સાથે જોડવામાં આવેલ છે. જ્યારે કળ ' $K$ ' બંધ હોય છે, ત્યારે આ સંયોજન સમાંતર સંગ્રહિત કુલ ઊર્જા $E_1$ છે. હવે કળ ' $K$ ' ને ખોલવામાં આવે છે અને $5$ જેટલો ડાયઈલેકટ્રીક અચળાંક ધરાવતા ડાયઈલેકટ્રીક માધ્યમને સંધારકોની પ્લેટો વચ્ચે દાખલ કરવામાં આવે છે. આ સંયોજનને સમાંતર સંગ્રહ પામતી કુલ ઊર્જા હવે $E_2$ થાય છે. ગુણોત્તર $E_1 / E_2 \ldots$ થશે.View Solution
- 7જો $V$ વોલ્ટના ઉદગમ સાથે $n$ કેપેસિટરો સમાંતરમાં જોડેલા હોય, તો સંગ્રહિત ઊર્જા બરાબર ........View Solution
- 8એક સમાંતર પ્લેટ કેપેસીટરની પ્લેટની લંબાઈ $l$ અને પહોળાઈ $w$ અને બે પ્લેટ વચ્ચેનું અંતર $d$ છે. તેને $V$ $emf$ ધરાવતી બેટરી સાથે જોડેલ છે. $d$ જાડાઈ અને $k =4$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતો એક સ્લેબ કેપેસીટરની બે પ્લેટ વચ્ચે દાખલ કરવામાં આવે છે સ્લેબને પ્લેટની અંદર કેટલી લંબાઈ સુધી દાખલ કરવો જોઈએ કે જેથી કેપેસીટરમાં સંગ્રહ પામતી ઉર્જા શરૂઆતની સંગ્રહિત ઉર્જા કરતાં બમણી થાય?View Solution
- 9શૂન્યાવકાશમાં $3\, cm$ તથા $1\, cm$ ત્રિજ્યાવાળા ગોળાને એકબીજાથી $10\, cm$ અંતરે રાખેલ છે જો દરેક ગોળાઓને $10\, V$ જેટલો વિદ્યુતભારીત કરવામાં આવે તો તેમની વચ્ચેનું અપાકર્ષણ બળ....View Solution
- 10બે અલગ અલગ $\frac{2}{3} R$ અને $\frac{1}{3} R$ ત્રિજ્યા ધરાવતા $S_{1}$ અને $S_{2}$ વાહક ગોળા પર અનુક્રમે $12\, \mu C$ અને $-3\, \mu C$ જેટલો વિજભાર છે અને બંને એકબીજાથી ખૂબ જ લાંબા અંતરે છે. તેને હવે એક વાહક તારથી જોડેલા છે. તેના પછી લાંબા સમયે $S_{1}$ અને $S_{2}$ પરનો વિજભાર કેટલો હશે?View Solution
