ધારોકે \(R_1 (=3\ cm)\) અને \(R_2(=1\ cm)\) ત્રિજ્યાવાળા ગોળા પર વિદ્યુત ભારો \(Q_1\) અને \(Q_2\) છે .
\(\therefore {V_1}\,\, = \,\,\frac{1}{{4\pi {\varepsilon _0}}}\,\frac{{{Q_1}}}{{{R_1}}}\,\, \Rightarrow \,\,10\,\, = \,\,\frac{{9 \times {{10}^9} \times {Q_1}}}{{3 \times {{10}^{ - 2}}}}\,\, \Rightarrow \,\,{Q_1}\,\, = \,\,\frac{{10 \times 3 \times {{10}^{ - 2}}}}{{9 \times {{10}^9}}}\)
અને \({V_2}\,\, = \,\,\frac{1}{{4\pi {\varepsilon _0}}}\frac{{{Q_2}}}{{{E_2}}}\,\, \Rightarrow \,\,10\,\, = \,\,\frac{{9 \times {{10}^9} \times {Q_2}}}{{1 \times {{10}^{ - 2}}}}\,\, \Rightarrow \,\,{Q_2}\,\, = \,\,\frac{{10 \times 1 \times {{10}^{ - 2}}}}{{9 \times {{10}^9}}}\)
કુલંબના નિયમ મુજબ,તેમની વચ્ચેનું અપાકર્ષણ બળ
\( = \,\,\frac{{9 \times {{10}^9} \times 10 \times 3 \times {{10}^{ - 2}} \times 10 \times 1 \times {{10}^{ - 2}}}}{{9 \times {{10}^9} \times 9 \times {{10}^9} \times {{(10 \times {{10}^{ - 2}})}^2}}}\,\)
(પરિણામ \(1\) અને \(2\) પરથી ) \( = \,\,\left( {\frac{1}{3}} \right) \times {10^{ - 9}}\ N\)
Download our appand get started for free
Similar Questions
- 1$R$ અને $4 R$ ત્રિજયાના સમકેન્દ્રિય ધાત્વિય ગોળીય કવચ પર અનુક્રમે $Q _{1}$ અને $Q _{2}$ વિજભાર છે. બંને સમકેન્દ્રિય ધાત્વિય ગોળીય કવચની પૃષ્ઠ વિજભાર ઘનતા સમાન હોય તો તેમના વિદ્યુતસ્થિતિમાનનો તફાવત $V ( R )- V (4 R )$ કેટલો હશે?View Solution
- 2$2 \;F$ સંધારકતા ધરાવતા એક સમાંતર પ્લેટ સંધારકને $V$ સ્થિતિમાન સુધી વિદ્યુતભારિત કરવામાં આવે છે. સંધારકમાં સંગ્રહિત ઊર્જા $E_1$ છે. આ સંધારક બીજા સમાન અવિદ્યુતભારિત સંધારક સાથે સમાંતરમાં જોડવામાં આવે છે. આ સંયોજનમાં સંગ્રહિત ઊર્જા $E_2$ છે. ગુણોત્તર $E _2 / E _1$ ........ થશે.View Solution
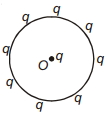
- 3આકૃતિમાં દર્શાવ્યા મુજબ એક બિંદુવત વિદ્યુતભાર $q$ને અન્ય આઠ બિંદુવત વિદ્યુતભાર દ્વારા $r$ જેટલા અંતરે છે. કેન્દ્ર સ્થાને રહેલાં વિદ્યુતભારને અનંત અંતરે ધકેલી દેવા માટેનું અપાકર્ષણ બળ વડે કુલ કેટલું કાર્ય કરવું પડે?View Solution
- 4એક નળાકારીય કેપેસિટર પાસે $1.4\,cm$ અને $1.5 \,cm$ ત્રિજ્યાના અને $15\,cm$ લંબાઈ ધરાવતા બે નળાકારો છે. બાહ્ય નળાકારને જમીન સાથે જોડેલ છે. અને અંદરના નળાકારને $3.5\ \mu C$ નો વિદ્યુતભાર આપેલ છે. તંત્રનો કેપેસિટન્સ અને અંદરના નળાકારનો સ્થિતિમાન અનુક્રમે. . . . . .View Solution
- 5View Solutionજ્યારે સમાંતર પ્લેટ કેપેસિટરની પ્લેટો વચ્ચે એક ડાઈ ઈલેકટ્રીક માધ્યમના ચોસલાને મુકવામાં આવે છે જેને બેટરી સાથે જોડતા તેમાં નવો વિદ્યુતભાર .....
- 6હવામાં સમકેન્દ્રીય રીતે $a$ અને $b (b > a)$ ત્રિજ્યા ધરાવતા બે ગોળાકાર કેપેસિટર $A$ અને $B$ ને મૂકેલો છે. $B$ ને $+ Q$ ધન વિદ્યુતભાર આપેલ છે. અને $ A$ જમીન સાથે જોડેલ છે. તો તેઓનો સમતુલ્ય કેપેસિટન્સ ?View Solution
- 7View Solutionસમાન વિદ્યુતક્ષેત્રમાં વિદ્યુત ડાઈપોલ માટે ન્યૂનત્તમ સ્થિતિ ઊર્જાની શરત ...... છે.
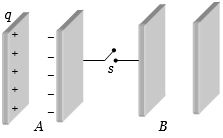
- 8કળ બંધ કરતાં $B$ કેપેસિટર પર વિદ્યુતભાર કેટલો થાય?View Solution
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે $A$ ક્ષેત્રફળ ધરાવતી દરેક ત્રણ સમાંતર ધાતુની પ્લેટો મુકેલી છે અને $Q_1$, $Q_2$ અને $Q_3$ વિદ્યુતભારો તેઓને આપવામાં આવે છે. છેડા (ધાર) પરની અસરો નગણ્ય છે. તો સૌથી બહારની બે સપાટીઓ $'a'$ અને $'f'$ પરનો વિદ્યુતભાર ગણો.View Solution
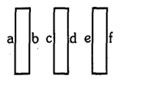
- 10આકૃતિમાં દર્શાવ્યા મુજબનો આલેખ વિદ્યુતક્ષેત્રની તીવ્રતા $E$ ને અંતરના $x$ નાં સાપેક્ષે દર્શાવેલ છે. ઉગમબિંદુ $O$ થી $x=2\,m$ અને $x=6\,m$ પરનાં બિંદુઓ વચ્ચે સ્થિતિમાનનો તફવવત $\dots\dots V$ હશે.View Solution